1. Introdução
A sustentabilidade na gestão dos negócios é uma estratégia fundamental a ser seguida por todas as organizações. No Brasil, nas indústrias voltadas ao processamento de alimentos, essa preocupação deve ser ainda maior, pois se estima que R$ 12 bilhões sejam desperdiçados anualmente, equivalendo a 1,4% do Produto Interno Bruto (PIB), saldo esse suficiente para alimentar 30 milhões de pessoas carentes. Aproximadamente, 64% daquilo que é plantado no Brasil, são desperdiçados ao longo da cadeia produtiva e, a distribuição dessas perdas, dá-se da seguinte forma: 20% na colheita, 8% no transporte e armazenamento, 15% na indústria de processamento, 1% no varejo e 20% no processamento culinário (Akatu, 2004).
No último processo dessa cadeia produtiva, é que se enquadram as Unidades de Alimentação e Nutrição (UANs), que segundo Lanzillotti et al. (2004), são locais destinados para a preparação e fornecimento de refeições equilibradas em nutrientes, considerando o perfil dos clientes a serem atendidos. Conforme Ricarte et al. (2008), os desperdícios em UANs variam desde alimentos que não são utilizados, até preparações prontas que não são servidas e as sobras recolhidas dos pratos dos clientes. Assim, três importantes indicadores na gestão das UANs são: o resto ingestão (IR), que indiretamente avalia a qualidade dos serviços oferecidos, tendo em vista este não ter sido consumido pela clientela; as sobras (IS), originadas da produção de alimentos não distribuídos à clientela; e o total dos desperdícios (IDA), que é a soma dos dois últimos (Nonino-Borges et al., 2006).
Segundo a Associação Brasileira das Empresas de Refeições Coletiva (Aberc, 2013), o mercado de refeições coletivas de prestadoras de serviços produz 11,7 milhões de refeições por dia. As prestadoras de serviços são contratadas por outras organizações para que ofereçam o serviço de refeição coletiva, sendo o seu faturamento oriundo do número de refeições servidas. Considerando a crescente preocupação com a sustentabilidade das ações organizacionais e a competitividade neste crescente mercado, faz-se necessário que as empresas desenvolvam sistemas de gestão que controlem adequadamente as perdas geradas nos processos. Todavia, o controle das variáveis envolvidas nas perdas é algo que, sem o apoio de ferramentas e metodologias apropriadas, torna-se algo empírico, sem a real capacidade de medir adequadamente em que situação a organização se encontra ou o quanto de melhoria os esforços despendidos têm contribuído.
Neste sentido, o presente artigo visa demonstrar a utilização do CEQ na gestão de desperdícios relacionados ao processamento culinário, e para tanto, apresenta um estudo de caso em uma UAN do interior do Estado do Rio Grande do Sul. A empresa em questão é uma prestadora de serviços para uma organização de grande porte, localizada na cidade de Teutônia e, desde o ano de 2011, vem monitorando diariamente os indicadores: resto ingestão e sobras de alimentos, por meio da pesagem de todos os restos obtidos dos pratos dos clientes ou comensais (que compõem o primeiro indicador) e dos restos obtidos das cubas e dos processos pelo qual os alimentos passaram (que compõem o segundo indicador). Neste sentido, foram então elaborados os índices per capita para cada indicador (IR, IS e IDA, respectivamente), que leva em conta o número total de clientes em cada período, e foram obtidos e analisados 61 dados históricos dos respectivos indicadores, sendo estes referentes ao período de agosto a setembro de 2012.
Segundo Montgomery (1997), o CEQ é um conjunto de ferramentas utilizadas para a gestão e melhoria dos aspectos que envolvam a qualidade dos produtos e serviços, baseado nos gráficos de controle desenvolvidos e implementados inicialmente por Shewhart (1924). A utilização dessa ferramenta auxilia a distinguir os momentos em que o processo está daquele em que o processo não está sob controle estatístico, permitindo ao gestor a análise e intervenção no processo para ajuste dos fatores que estejam influenciando, caso o resultado seja indesejado (Aliverdi et al., 2013). Segundo Müller (2008), são vários os fatores que possivelmente geram desperdícios nas UANs, por exemplo: frequência diária de usuários, preferências alimentares, planejamento inadequado da quantidade de refeições a serem produzidas, capacitação dos funcionários na produção e no porcionamento, entre outros. Além disso, o CEQ auxilia também na análise do atendimento às metas e no benchmarking de processos, que é viabilizado utilizando-se os índices de capacidade.
Para tanto, o artigo encontra-se dividido conforme a seguinte estrutura: na Seção 1 está a introdução, o tema, a justificativa e os objetivos do presente estudo de caso; na Seção 2 apresenta-se a fundamentação teórica, abordando o CEQ, seus pressupostos teóricos e os gráficos XmR e MR; na Seção 3, a metodologia utilizada para a análise dos dados via CEQ; na Seção 4, apresenta-se o desenvolvimento do estudo de caso, onde os dados obtidos são analisados via gráficos de controle supracitados e os índices de desempenho do processo; na Seção 5 apresenta-se um modelo para a aplicação do CEQ em UANs; e, na Seção 6, apresenta-se as considerações finais do estudo, bem como sugestões de trabalhos futuros.
2. Controle Estatístico de Qualidade (CEQ)
A qualidade tem sido considerada um fator decisivo na escolha dos produtos e serviços e, neste sentido, tem sido constante a busca por métodos de controle de qualidade que possam colaborar para sua melhoria. Estudos para a otimização dos gráficos de controle, o desenvolvimento de novas metodologias para a sua construção e a aplicação destas técnicas em áreas o qual ainda não foram aplicados, são exemplos dos esforços despendidos (Ho; Quinino, 2013). Destaca-se que todos os processos, de manufatura ou de serviços, exibem variabilidade e, quanto maior for essa variabilidade, maior será o seu descontrole em relação aos resultados produzidos e os resultados desejados (Juran; Gryna, 1992; Montgomery, 1997). Por sua vez, esta variabilidade pode ser classificada em duas situações: (i) devido às causas comuns, ou aleatórias; e, (ii) devido às causas assinaláveis, ou especiais. O controle estatístico de processo (CEP) tem como objetivo diferenciar as causas assinaláveis das causas comuns para realizar ação sob o processo, mantendo-o sob controle e promovendo um ciclo de melhoria contínua (Aliverdi et al., 2013).
Caso identificada a presença de causas especiais influenciando os resultados do processo, procede-se a realização de uma investigação com a finalidade de removê-las. Essa etapa utiliza diversas ferramentas da qualidade para uma adequada identificação, dentre elas, o brainstorming, o diagrama de causa e efeito, o gráfico de Pareto e o gráfico de dispersão (Juran; Gryna, 1992). Essa ação sistemática de identificação de desvios, análise das causas e ação de correção, gera um ciclo de melhoria contínua e é o fundamento do CEQ.
O diagrama de causa e efeito ou diagrama de Ishikawa é uma ferramenta comumente utilizada no CEQ. Segundo Lins (1993), esse diagrama é utilizado quando for necessário identificar a causa raiz de um problema, pois o mesmo permite, a partir dos grupos básicos de possíveis causas, desdobrá-las até os níveis de detalhe adequados à solução do problema. Os grupos básicos variam conforme o tipo de problema analisado, se operacional ou gerencial, por exemplo. Para o primeiro caso, sugerem-se os seguintes grupos: máquinas, materiais, mão de obra, metodologias/métodos e instalações/ambientes. Para o segundo caso, sugerem-se os seguintes grupos: políticas, equipamentos, pessoas/recursos humanos, procedimentos e infraestrutura. Na Figura 1 é apresentado um diagrama de Ishikawa exemplificando alguns dos fatores que podem influenciar na gestão dos desperdícios das UANs ou, quando o IDA é maior que os limites de controle superior (Eqs. 5 e 8).
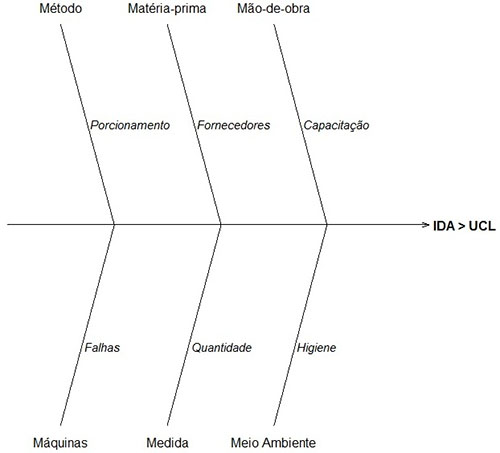
Figura 1 – Aplicação do diagrama de causa efeito a um problema operacional da UAN.
Fonte: Elaborado pelos autores (2013) a partir de Lins (1993) e Müller (2008).
2.1 Análise do desempenho do processo e pressupostos para a utilização do CEP
Além da identificação de causas especiais atuando no processo, o CEP dispõe de ferramentas para análise sobre o seu desempenho ao longo do tempo. A análise do desempenho através do CEP consiste no quanto o processo consegue atender às especificações dos produtos ou serviços. A técnica mais conhecida para a análise do desempenho dos processos são o Pp e o Ppk, apresentados nas Equações 1 e 2, respectivamente. Considera-se capaz o processo que apresentar Ppk maior que 1,33; razoável aquele que apresentar Ppk maior que 1 e menor que 1,33; e, incapaz aquele que apresentar Ppk menor que 1 (Costa et al., 2004).
![]()
![]()
Onde:
LSE= limite superior de especificação;
LIE= limite inferior de especificação;
S= desvio padrão do processo;
![]() média do processo.
média do processo.
Porém, para a utilização adequada do CEP, há de se ter atenção aos pressupostos estatísticos básicos. Tendo em vista que esta ferramenta foi criada com base em teorias de probabilidade, a sua não observância faz com que os resultados gerados não sejam válidos para a análise desejada (Moraes et al., 2006). Segundo Montgomery (1997) são dois os pressupostos básicos para a utilização dos gráficos de controle: as observações devem ser independentes e identicamente distribuídas e, as observações devem seguir alguma distribuição de probabilidade específica (normal, binomial ou Poisson, por exemplo). Esses dois pressupostos são a base para a definição dos limites de controle e para as regras para identificação de padrões não aleatórios. No caso dos índices Pp e Ppk, estes somente poderão ser analisados após a confirmação do processo estar sob controle estatístico, sendo esse o seu pressuposto básico (Costa et al., 2004).
Korzenowski (2009) apresenta os seguintes testes como forma de verificação dos pressupostos descritos por Montgomery (1997): (i) para a verificação de normalidade, o autor recomenda os testes de Shapiro-Wilk e/ou o teste de Anderson-Darling; (ii) para a verificação da independência dos dados, os testes recomendados são o teste de hipóteses das carreiras, o teste d de Durbin-Watson, a análise da função de autocorrelação (FAC) ou da função de autocorrelação parcial (FACP), e as estatísticas de Box-Pierce e Ljung-Box. Caso seja verificada a não aderência à distribuição normal dos dados, Juran e Gryna (1992) e Moraes, et al. (2006), recomendam os seguintes critérios de análise para a utilização dos dados coletados:
- Examinar os dados, para verificar se há alguma explicação não estatística para o padrão distribucional não convencional;
- Analisar os dados em termos de médias, em vez de valores individuais, pois médias de amostras seguem uma distribuição de probabilidade normal, mesmo se a população de valores individuais não é distribuída normalmente (teorema do limite central);
- Utilizar como referência outro tipo de distribuição, que se enquadre mais adequadamente ao conjunto de dados coletados;
- Efetuar transformação matemática da característica original, para uma nova característica que se aproxime de uma distribuição normal.
Há diversas distribuições para utilização no CEP, distribuições tanto para dados contínuos quanto para dados discretos, por exemplo: binomial, Poisson, hipergeométrica, Log-normal, beta, Weibull, entre outras. Caso seja optado pela transformação matemática dos dados, conforme alínea d anterior, dois métodos são comumente utilizados: a transformação de Box-Cox e a transformação de Yeo-Johnson. Para maiores detalhes sobre tais transformações e sua utilização, recomenda-se consultar o trabalho de Moraes et al. (2006).
O outro pressuposto, que trata da independência dos dados, conforme anteriormente citado, pode ser verificado também através da FAC. A Equação 3 apresenta a estimativa do coeficiente de autocorrelação amostral de defasagem ou lag k (Makridakis et al., 1998). O conjunto de valores de é denominado FAC e a representação gráfica deste conjunto de valores em relação a seus lags é o correlograma da FAC (Matos, 2000; Fava, 2000). A estatística é uma ferramenta amplamente utilizada nos modelos de Box e Jenkins (1970) para séries temporais e descreve a correlação entre dois valores de determinada variável, em diferentes períodos de tempo (Enders, 2004).
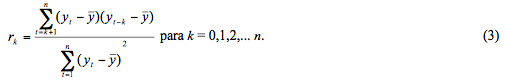
A estatística de Ljung-Box permite testar com mais precisão se os k primeiros coeficientes de autocorrelação são conjuntamente iguais à zero. A Equação 4 apresenta o teste para os K coeficientes. O teste segue a distribuição com k graus de liberdade. A conclusão é realizada por meio da comparação entre as seguintes estatísticas: se , rejeita-se a hipótese de que os K primeiros coeficientes de autocorrelação são iguais a zero e vice-versa (Fava, 2000).
![]()
Onde:
rk: coeficiente amostral de autocorrelação do lag k;
k: lag de ordem k;
n: número de elementos na amostra;
y1: variável y (que se deseja controlar) no período t;
y: média amostral da variável y;
yt-k: variável y defasada no período t-k;
Q(K): estatística de Ljung-Box para os K primeiros coeficientes rk;
K: conjunto dos K primeiros coeficientes rk.
Caso seja verificada a presença de autocorrelação nos dados, recomenda-se realizar a modelagem de um ARIMA (Autoregressive Integrated Moving Average), obter os resíduos da modelagem e então aplicar os gráficos de controle nestes resíduos. Maiores detalhes para a realização desses procedimentos podem ser verificados nos trabalhos de Box e Jenkins (1970), Montgomery (1997) e Moreira Júnior (2005).
2.2 Limites de controle para os gráficos de medidas individuais XmR e MR
O controle de medidas individuais é realizado por intermédio de dois gráficos: o XmR e o MR. O gráfico de controle XmR monitora se uma causa especial de variação está presente em cada amostra. O segundo gráfico, ou o moving range (MR), monitora a variação entre duas amostras consecutivas. As Equações 5-10 apresentam o cálculo das medidas dos dois gráficos e seus limites de controle superior (UCL) e inferior (LCL), respectivamente (Aliverdi et al., 2013; Montgomery, 1997).
![]()
![]()
![]()
![]()
![]()
![]()
Onde é cada medida individual da variável em análise e é a amplitude móvel. No caso do presente estudo, os parâmetros dos gráficos são os seguintes: , , e (Aliverdi et al., 2013).
3. Metodologia
Na Seção 3 é apresentada a metodologia utilizada para a realização deste estudo de caso. Os dados coletados são referentes ao período de agosto a setembro de 2012, totalizando 61 valores de sobras dos seguintes alimentos: arroz, feijão, guarnição, saladas e carnes; e dos restos ingestão, obtidos nos pratos dos clientes. Os dados foram coletados diariamente utilizando balança com capacidade de 20Kg e precisão de 0,005Kg, sendo esses oriundos do período da refeição. Para tanto, foi desenvolvido um índice per capita do total de desperdícios de alimentos (Equação 11), para que seja possível o monitoramento global e estratificação dos dados em caso de causas especiais influenciando o processo.
![]()
Onde:
IDA1: índice per capita de desperdício de alimentos em i (gramas/pessoa/refeição);
SA1: sobras de arroz no período i (gramas/refeição);
SF1: sobras de feijão no período i (gramas/refeição);
SG1: sobras da guarnição no período i (gramas/refeição);
SS1: sobras de saladas no período i (gramas/refeição);
SC1: sobras de carne no período i (gramas/refeição);
SR1: soma dos restos ingestão no período i (gramas/refeição);
NPR1: número de refeições previstas e produzidas no período i (pessoa/refeição/dia);
NPS1: número de refeições servidas no período i (pessoa/refeição/dia).
Em seguida, os dados foram analisados para a verificação do atendimento aos pressupostos estatísticos para a utilização dos gráficos de controle e para a análise do desempenho do processo em atender às metas estabelecidas. Para tanto, as seguintes etapas foram realizadas: (i) foi analisada a condição de normalidade dos dados por meio do teste de Anderson-Darling; (ii) por meio da FAC e da estatística de Ljung-Box, foi analisado se os dados são considerados independentes; (iii) foram calculados os limites de controle superior, inferior e as medidas individuais (índices per capita de desperdício de alimentos) para os gráficos XmR e MR; (iv) para a análise do desempenho do processo, foram eliminados todos os pontos fora de controle observados nos gráficos XmR e MR e então foram calculados os indicadores Pp e Ppk e as medidas descritivas de cada amostra. Com base na metodologia utilizada, foi desenvolvido um modelo para a aplicação do CEQ na gestão dos desperdícios de alimentos em UANs.
4. Resultados
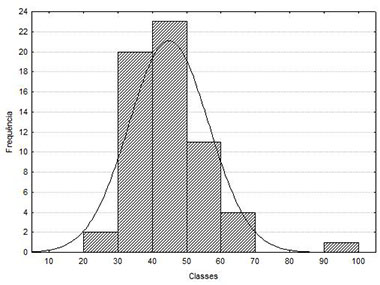
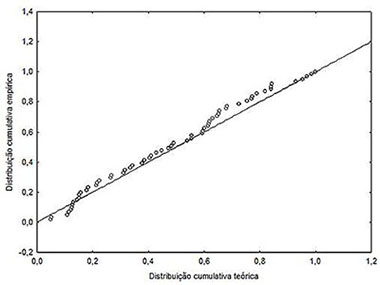
O teste de normalidade de Anderson-Darling para o IDA, ao nível de 10%, indicou que a amostra de dados provém de uma distribuição normal (p-valor = 0,0725). Na Figura 2, observa-se o histograma e o gráfico de probabilidade para os dados amostrais.
|
|
Figura 2 – Histograma (a) e PP-plot do IDA do período em análise (b).
Atendida a situação de normalidade dos dados, foi então verificado o atendimento ao pressuposto de independência ou não autocorrelação. Na Figura 3 pode-se observar o correlograma da FAC dos dados amostrais do IDA. Observa-se que nenhum dos coeficientes amostrais de autocorrelação ultrapassou o intervalo de confiança estabelecido para o nível de 5% de significância, concluindo então pela ausência de autocorrelação.
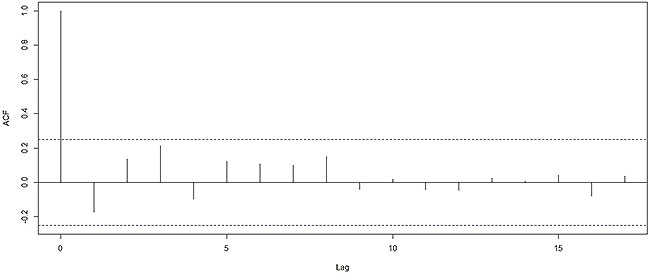
Figura 3 – Correlograma da FAC para o IDA do período analisado.
Portanto, ao nível de 5% de significância, os dados amostrais são considerados normais e independentes (Q(10)=11,06 < =18,31, conforme a estatística de Ljung-Box), passíveis então de serem analisados via gráficos de controle para medidas individuais. Foram então construídos os gráficos de controle XmR e os seus limites de controle superior e inferior, (conforme as Eqs. 5 e 7) utilizando a biblioteca qcc do pacote estatístico R (R Development Team, 2013). Na Figura 4 observa-se o gráfico de controle para as medidas individuais do IDA.
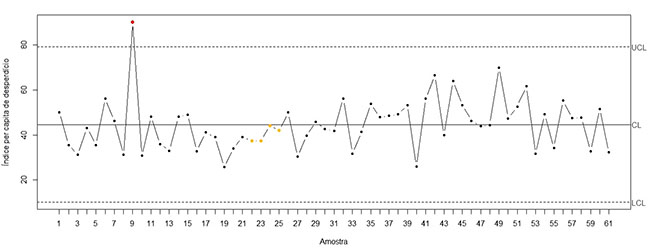
Figura 4 – Gráfico de controle XmR para o índice per capita de desperdício de alimentos.
Na Figura 4 verifica-se o gráfico de controle XmR para o IDA. Observam-se duas situações distintas ocorridas no período em análise, que são: (i) a amostra ultrapassou o limite superior de controle (UCL=79,5); e, (ii) as amostras 23-25 violam a suposição de aleatoriedade dos dados, pois 3 ou mais medidas consecutivas encontram-se localizadas no primeiro desvio-padrão. Ambas as situações demonstram a necessidade de intervenção no processo, pois causas especiais o estão influenciando, havendo o risco de um descontrole maior do processo como um todo.
Na Figura 5 observa-se o gráfico de controle da amplitude móvel (MR) dos dados. Trata-se de um gráfico que complementa a análise realizada para os dados individuais reais, o qual monitora a amplitude entre os IDAs. No presente caso, não foram observadas as situações descritas para o gráfico da Figura 4. Porém, esse fato não eliminaria a necessidade de análise das causas que estariam influenciando e os respectivos ajustes que seriam necessários ao processo. Conforme o gráfico da Figura 5, o quase causou um descontrole do processo.

Figura 5 – Gráfico de controle da amplitude móvel (MR) para o índice per capita de desperdício de alimento.
Por fim, foram calculadas as medidas descritivas: média, mediana, desvio-padrão, coeficiente de variação, mínimo e máximo; para os índices per capita: IS, IR e IDA. Os chamados limites superior (LSE) e inferior de especificação (LIE), conforme conhecido na literatura do CEQ, aqui foi entendido como a meta máxima admissível pela UAN para o IDA (em gramas/pessoa/dia), considerando a avaliação por parte da direção da empresa. Na Tabela 1 são apresentados os resultados das medidas descritas neste parágrafo.
Tabela 1 – Análise descritiva e de desempenho dos dados amostrais
Análise descritiva |
IS |
IR |
IDA |
Média (g/pessoa/dia) |
21,7 |
23,0 |
44,7 |
Mediana (g/pessoa/dia) |
20,8 |
21,3 |
44,2 |
Desvio padrão (g/pessoa/dia) |
6,8 |
7,9 |
11,5 |
Coeficiente de variação (%) |
32,0 |
34,5 |
26,1 |
Mínimo (g/pessoa/dia) |
5,2 |
8,4 |
25,7 |
Máximo (g/pessoa/dia) |
40,8 |
55,6 |
90,1 |
LSE (g/pessoa/dia) |
17,5 |
17,5 |
35,0 |
LIE (g/pessoa/dia) |
5,0 |
5,0 |
10,0 |
Pp (adimensional) |
0,31 |
0,26 |
0,58 |
Ppk (adimensional) |
-0,21 |
-0,12 |
0,15 |
Os índices de desempenho Pp e Ppk demonstram que o processo, apesar de na maior parte do tempo estar sob controle estatístico, não é capaz de atender às metas estabelecidas, sendo necessárias ações para redução da variabilidade. O LSE representa a meta máxima de desperdício que a empresa assume como adequado, sendo para o presente caso a quantidade de 35 gramas/pessoa/dia para o caso do IDA. O LIE adotado é igual a 10 gramas/pessoa/dia, pois esse é o valor pelo qual se acredita ser o valor mínimo a ser buscado, considerando que os esforços necessários para obter valores menores ainda, não apresentaria uma relação de custo e benefício satisfatória.
5. Modelo para gestão dos desperdícios em UANs por meio de CEQ
Na Seção 5 apresenta-se um modelo para a gestão dos desperdícios de alimentos em UANs, baseado nas técnicas e ferramentas de CEQ e na metodologia abordada no presente estudo. O modelo proposto baseia-se em cinco processos principais, que são: (i) a coleta periódica dos dados que compõem o IDA; (ii) a verificação periódica dos dados quanto aos pressupostos a serem atendidos; (iii) a modelagem dos dados segundo a técnica de CEP adequada; (iv) a investigação das causas especiais que estejam influenciando no processo; e, (v) o monitoramento dos dados e análise periódica da performance do processo.

Figura 6 – Modelo para a gestão dos desperdícios de alimentos em UANs.
A etapa de coleta dos dados consiste em registrar diariamente os desperdícios em termos de sobra e em termos de resto ingestão. Os dados de sobra de alimentos são obtidos através da pesagem de todos os alimentos desperdiçados ao longo do processo de produção e dos alimentos oferecidos nos buffets, que não serão reaproveitados posteriormente. Os dados de resto ingestão são obtidos através da pesagem de todos os restos retirados dos pratos dos comensais, não sendo este, ao contrário do anterior, categorizado conforme o tipo de alimento. O IDA é obtido através da soma do IS e do IR (Equação 11). Na Figura 7 apresenta-se um modelo para a coleta e registro dos dados de desperdício de alimentos.

Figura 7 – Coleta dos dados de desperdício para a composição dos indicadores.
A verificação dos pressupostos, conforme já delineado, é realizada por meio dos testes de normalidade e de independência dos dados amostrais. Caso não atendido os pressupostos básicos, são realizados os procedimentos discutidos na Seção 2. O controle é realizado por meio do IDA do período i, sendo este, portanto, analisado via gráficos de controle apresentados nas Seções 2 e 4. Caso necessário, o IS e o IR também podem ser monitorados individualmente via CEP, garantindo um controle mais efetivo do processo.
A quarta etapa consiste da análise dos casos em que os gráficos de controle mostram a presença de causas especiais influenciando o processo. Nesta etapa, utilizam-se as ferramentas clássicas da área de qualidade para a busca da causa raiz dos desvios, dentre elas: o diagrama de causa e efeito (conforme Figura 1), a estratificação de Pareto, brainstorming, check-lists, entre outras ferramentas necessárias para controle dos desvios. Para o tratamento dos desvios, recomenda-se a utilização de uma abordagem estruturada, que irá auxiliar em uma implementação e controle mais eficiente, como por exemplo, o método planejar-realizar-checar-agir (PDCA) (Campos, 1998).
Por fim, caso não haja causas especiais atuando sobre o processo, é importante monitorar periodicamente o mesmo, evitando que situações indesejadas passem a acontecer. Periodicamente (semanal ou mensalmente) é importante realizar análises de desempenho do processo, verificando o quanto este é capaz de atingir as metas estabelecidas pela administração, para que as respectivas ações sejam tomadas com o intuito de melhorar continuamente os processos.
6. Considerações Finais
O presente artigo apresentou um estudo de caso utilizando o controle estatístico de qualidade como ferramenta de suporte para a gestão de desperdício de alimentos em uma unidade de alimentação e nutrição. Para tanto, os indicadores a serem gerenciados foram estabelecidos, foram coletadas amostras para a realização de uma análise do processo atual utilizando o CEP, foram realizadas as análises e, finalmente, foi apresentado um modelo genérico para a gestão do desperdício de alimentos em UANs por meio do CEQ. O indicador analisado no estudo foi o índice de desperdício de alimentos, que representa, de forma global, o índice per capita de desperdício de alimentos na UAN em estudo no período considerado.
Verificou-se que o IDA apresentou normalidade e independência nos dados da amostra considerada, não havendo necessidade de transformação, ou utilização de modelos de séries temporais para a sua modelagem ou, ainda, não se faz necessária a busca por outra distribuição de probabilidade que descreva os dados. Verificou-se, após a análise dos gráficos de controle, que em 5 momentos houve presença de causas especiais atuando no processo, estando, portanto, 91,8% do tempo analisado sob controle estatístico.
Em contrapartida a aparente boa performance do processo, as medidas descritivas e a análise por intermédio dos índices de desempenho, indicaram que o processo não apresenta capacidade para atingir adequadamente as metas máximas de desperdícios estabelecidas pela direção da empresa. Verificou-se a necessidade de redução da variabilidade global do processo, que foi de 26,1%, e da média global do processo, que foi de 44,7 gramas por pessoa por dia.
Quanto ao modelo apresentado na Seção 5, verificou-se que esse é capaz de atender às necessidades dos gestores das UANs, pois apresenta uma metodologia clara, padronizada e com base estatística para que o desempenho dos processos existentes possa ser controlado. A implantação desse modelo é capaz de auxiliar as UANs na busca por maior qualidade dos serviços oferecidos, redução dos custos de processo por meio da redução de desperdícios de matéria-prima e alimentos processados, e colabora para uma estratégia de sustentabilidade do negócio, tendo em vista as questões éticas envolvidas na indústria de processamento culinário.
Para a realização de trabalhos futuros, sugere-se a utilização de gráficos de controle com maior capacidade de detecção de causas especiais, como por exemplo: o Cumulative Sum (CUSUM) e o Exponentially Weighted Moving Average (EWMA) (Vargas et al., 2004).
Referências Bibliográficas
Aberc. Mercado Real. São Paulo. Acessado em 29 de junho de 2013. Disponível em: http://www.aberc.com.br/mercadoreal.asp?IDMenu=21.
Akatu. Anutrição e o consumo consciente – Caderno temático. Acessado em 13 de julho de 2013. Disponível em: http://www.akatu.org.br/Content/Akatu/Arquivos/file/nutricao(2).pdf.
Aliverdi, R.; Naeni, L. M.; Salehipour, A. (2013); “Monitoring project duration and cost in a construction project by applying statistical quality control charts”, International Journal of Project Management, (31), 411-423.
Box, G. E. P.; Jenkins, G. (1970); Time Series Analysis: Forecasting and Control; San Francisco, Ed. Holden-Day.
Campos, V. F. (1998); Gerenciamento da rotina do trabalho do dia-a-dia; Belo Horizonte, Ed. DG.
Costa, A. F. B.; Epprecht, E. K.; Carpinelli, L. C. R. (2004); Controle estatístico de qualidade; São Paulo, Ed. Atlas.
Enders, W. (2004); Applied Econometric Time Series; New York, Ed. Wiley & Sons.
Fava, V. L. (2000); Análise de Séries de Tempo; In: Vasconcellos, M. A. S.; Alves, D. Manual de econometria: nível intermediário; São Paulo, Ed. Atlas.
Ho, L. L.; Quinino, R. C. (2013); “An attribute control chart for monitoring the variability of a process”, International Journal of Production Economics.
Juran, J. M.; Gryna, F. M. (1992); Controle da qualidade: métodos estatísticos clássicos aplicados à qualidade; São Paulo, Ed. Makron.
Lanzillotti, H. S.; Monte, C. R. V.; Costa, V. S. R.; Couto, S. R. M. (2004); “Aplicação de um modelo para avaliar projetos de unidades de alimentação e nutrição”, Nutrição Brasil, 3(1), 11-17.
Lins, B. F. E. (1993); “Ferramentas básicas da qualidade”, Ci. Inf., 22(2), 153-161.
Korzenowski, A. L. (2009); Premissas e suposições para construção de gráficos de controle: um framework para verificação. Dissertação – Programa de Pós-Graduação em Engenharia de Produção, Universidade Federal do Rio Grande do Sul,Porto Alegre.
Makridakis, S.; Wheelwright, S. C.; Hyndman, R. J. (1998); Forecasting:Methods and Applications; New York, Ed. Wiley & Sons.
Matos, O. C. M. (2000); Econometria básica: teoria e aplicações; São Paulo, Ed. Atlas.
Montgomery, D. C. (1997); Introduction to statistical quality control; New York, John Wiley & Sons.
Moraes, C. F.; Ferreira, J. R.; Balestrassi, P. P. (2006); “Análise crítica da aplicação de métodos estatísticos em processos definidos por dados que não apresentam distribuição normal”, Revista GEPROS, 1(2), 7-18.
Moreira Junior, F. J. (2005); Proposta de um método para o controle estatístico de processo para observações autocorrelacionadas. Dissertação – Programa de Pós-Graduação em Engenharia de Produção, Universidade Federal do Rio Grande do Sul,Porto Alegre.
Müller, P. C. (2008); Avaliação do desperdício de alimentos na distribuição do almoço servido para os funcionários de um hospital público de Porto Alegre – RS. Monografia – Graduação em Nutrição, Universidade Federal do Rio Grande do Sul, Porto Alegre.
Nonino-Borges, C. B.; Rabito, E. I.; Silva, K.; Ferraz, C. A.; Chiarello, P. G.; Santos, J. S.; Marchini, J. S. (2006); “Desperdício de alimentos intra-hospitalar”, Revista de Nutrição, 19(3), 349-356.
R Core Team (2012); R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.
Ricarte, M. P. R.; Moura Fé, M. A. B.; Santos, I. H. V. S.; Lopes, A. K. M. (2008); “Avaliação do desperdício de alimentos em uma unidade de alimentação e nutrição institucional em Fortaleza – CE”, Revista Saber Científico,1(2), 158-175.
Vargas, V. C. C.; Lopes, L. F. D.; Souza, A. M. (2004); “Comparative study of the performance of the CuSum and EWMA control charts”, Computers & Industrial Engineering, 46, 707-724.