1. Introduçtion
The growing demand for electricity and the depletion of freshwater resources in the world make clear the need for the inclusion of analytical methods able to represent and / or simulate the hydrologic behavior of a watershed in order to provide the natural water resources management, corroborates Yilmaz and Harmancioglu (2010); Tucci (1998).
The gradual increase in the predominance of hydroelectricity, in recent decades in Brazil and in the world, is related to the liberalization of energy markets, according to Lienert and Lochner (2012), given that the generating capacity, investment and energy prices, imply the energy potential of each hydroelectric power plant, where the information of the natural affluent flow of a watershed is a key input for planning and operating the hydroelectric park, according to Guilhon, Rocha e Moreira (2007).
The understanding, diagnosing and/or simulating the behavior of the confluence flow of a river, corroborated by Costa et al. (2007); Fadiga et al. (2008) is based on the use of hydrological models, whether stochastic or deterministic, empirical or conceptual, continuous or discrete, accurate or distributed, statistical or dynamical, if they configure as an additional support, in the optimization, operation and control of a hydroelectric power plant.
Xiong and Guo’s verifications (1999), in flow simulations of 70 sub-basins in southern China, reached good results, just as Lucas et al. (2009), for presenting a two-parameter monthly deterministic hydrologic model with a simpler structure compared to a four-parameter model used by Guo (1995). However, in each study region the evaluation of results by means of representative models is related not only to the ability of the model to capture the generating process of the time series, but also to factors such as: location of the watershed, soil texture, climatic, physical and biological properties.
According to Lucas et al. (2009), the application of stochastic and deterministic models to Brazilian hydrological series appeared to be efficient in planning and/or water resources management, efficiently simulating the monthly average flows of the region under study, where the deterministic model obtained a lower performance compared to the ARIMA stochastic model (Auto-Regressive Integrated Moving Average) in all seasons studied.
The investigation of the affluence flow of the Jaguari River is necessary due to its representativeness with the electricity generation in the region where it is located, since several agro-industries, manufacturing industries and other trade in general, beyond the urban and rural population who are assisted with the electricity generated through this watershed. The knowledge of its hydrological behavior subsidizes decision-makings in the water resources management, since this study will show the periods considered anomalous to the generating process.
Therefore, this study aims to analyze the average scheme and the flow variability of the Jaguari River, responsible for providing 6.2 MW-hour-month, by means of ARIMA stochastic models (Auto-Regressive Integrated Moving Average), and ARCH models (Auto-Regressive Conditional Heteroscedasticity), seeking information to assist hydroelectric generating and management, as well as to perform the interpretation of the persistence of anomalous periods if they occur.
Controlling variables involved in the production process, due to the high competitiveness in industry has made energy efficiency techniques to be adopted in national and international markets with the aim of strengthening the growing concern about environmental degradation and the energy matrix, where the adoption of statistical methods to process control is an efficient way to reduce waste and to maintain full capacity, this idea is corroborated by Jacobi, Souza and Pereira (2002), Silva, and Jabbour (2012).
This study is organized as follows: First section will present the importance of the study, the objectives and some prominent studies about the importance of the affluence flow in determining the potential of a hydroelectric power plant and the regional water resources management. Second section will present methodology, emphasizing the use of ARIMA and ARCH models and third section will present the results and discussions on the possible contributing factors to the variation of the affluence flow of the Jaguari River-RS.
2. Methodology
This study was made through the collection of the monthly historical series of flows in m3/s from 1942 to 2006, based on the database system of the 120 station, Southeast system, latitude: 29:21:32, longitude: 54:30:7, provided by the National System Operator (ONS). The Jaguari River is located between the geomorphologic units of the southern plateau and the southern depression, characterized by neossolo soils (sandy areas and hard fields) and planossolos (floodplains), respectively, with subshrubby field areas, remaining forest areas grassland areas, agricultural areas with extensive culture of soybean (summer) and soybean / wheat (winter) interspersed with pastures, according COREDE (2009); Righi and Robaina (2008).
Initially, the behavior of the original series is graphically inspected, and then the descriptive statistics regarding asymmetry, kurtosis, stationarity, normality, trend and seasonality are calculated. Later, the Augmented Dickey-Fuller (1984) - (ADF) and Kwiatkowski-Phillips-Schmidt-Shin (1992) - (KPSS) unitary root tests are applied, seeking to find a stationary series able to reflect the behavior of the affluence flow series.
The identification of the type and the order of the models are made through the autocorrelation function (FAC) and partial autocorrelation function (FACP), according to Morettin (2008); Lucas et al (2009), where FAC measures the degree, that is, how a value observed in period t is influenced by the value observed in period t-1. However, the FACP is defined by the following correlations over time (Zt; Zt-1), (Zt, Zt-2), (Zt, Zt-p), with constant previous lag effects over Zt. Once the stationarity of the series under study is checked, linear modeling takes place, following the iterative cycle proposed by Box and Jenkins (1970): identification; estimation; verification, according to Gujarati, (2000).
Among the models able to capture the behavior of the series under study Jacobs and Costa (2011), are the general ARIMA models, which exploit the structure of the autocorrelation between the affluence flows in consecutive stages, defined by:
(1)
Wherein 
represents the autoregressive part of the filter and 
represents the moving averages and at represents the random error. Given that Δd represents the differences (d) to turn the series into stationary, if necessary.
If the series presents autocorrelation in seasonal periods, according to Marchezan and Souza (2010), represented by a repetition period equal to S = 3, 6, 12, the ARIMA seasonal models are used, represented by SARIMA (p, d, q) (P, D, Q)s, where d is the representative part of simple differentiation and D is the representative part of seasonal differentiation, according to equation 2.
(2)
Wherein 
and 
represents the parameters of the seasonal model.
For the selection of competing models that explain the behavior of the affluence flow series, AIC criterion statistics are used (Akaike Information Criteria), according to Souza et al. (2010); Menezes, Souza and Souza (2011), choosing the lower statistic value model.
As the linear model showing residues with characteristics of white noise 
is found, the presence of conditional heteroscedasticity in the quadratic residuals of the linear model by means of the ARCH-LM statistic test is verified.
If the presence of conditional heteroscedasticity is evident, and in order to capture the intrinsic variability of the series, ARCH models proposed by Engle (1982) are applied, according to Ceretta et al. (2010), and it is considered that the conditional variance may change over time and is predicted by past errors squared, capturing an important stylized fact called groupings or volatility clusters. According to Morettin (2006); Souza, Souza and Menezes (2012), the ARCH model (m) is defined as follows:
(3)
Thus, it can be seen that the conditional variance of the error 
with regard to the available information for period (t-1) is distributed, according to equation 4.
(4)
In the case of an ARCH (1) model, the conditional variance is defined by equation 5.
(5)
Thus, it is expected that ARCH (1) modeling supposes residues identically distributed i.i.d., which were shown in equation 6.
(6)
The study made to assess the average level of the Jaguari River-RS, by means of Auto-Regressive Integrated Moving Averages (ARIMA) models, consists in exploring and/or capturing the behavior of serial correlation or autocorrelation among the affluence flows in successive stages, according to Vicini and Souza (2007). However, the Autoregressive Conditional Heteroskedascity (ARCH) models aim to characterize and analyze the monthly intrinsic volatility of the affluence flow series, in scope to estimate how long the oscillation, that is, the variability of the variance will take to temporize its return to its usual behavior. Therefore, it is intended to provide subsidies to the delineation of appropriate strategies for the regional water resources management under study and to analyze the potential flow for hydroelectric generation.
3. Results and Discussion
According to the hydrometeorological network of the National Water Agency (ANA), the annual spatial temporal variation rainfall of the Jaguari River, under code 02954005 ranged from 1136.3 mm to 2923 mm, from February to May 1991, and from July to December 2002. However, in the station under code 02954007, variation ranged from 963.5 mm in 2004, to 2797.7 mm in 2002, marking the same periods under code 02954005.
The oscillations of the affluence flows of the Jaguari River are related to the climatic, physical and biological characteristics of its ecosystems, according to Güldal and Tongal (2010). The amount of water that is lost through evapotranspiration, the nature and extent of geological formations, natural vegetation and interaction of species also contribute to the oscillation of the affluence flows of a watershed, corroborates Barros and Amin (2007), Rodrigues et al. (2010).
Among the probable causes of the increase and decrease of flow affluences of the Jaguari River are the effects of soil conservation, given that the techniques used for this purpose reflects an increase in groundwater recharge directly in the water source flows over the year, according to Gomes et al. (2012); human-induced actions can also change the water balance in local and regional scale as deforestation, irrigation projects, food and feed, among others.
This rainfall oscillation is related to the movement of the confluence flows of the Jaguari River, as shown in Figure 1, periods of high and low amplitude peaks, being linked to extreme weather, warm phase (El Niño) and cold phase (La Niña), which influences the climatic rhythm of Rio Grande do Sul, acting under the rhythm of displacement of the fronts, according to Britto et al. (2008).
According to Prina and Monguilhott (2011), a decrease by 16% of the total green area on the banks of the Jaguari River was observed, as shown in Figure 1, this decrease is possibly due to flooding and agricultural activities that damage the soil, for conservation practices are not being used, occasioning thus silting and decrease of the volume raised and reducing thus the affluence flow of the Jaguari River.
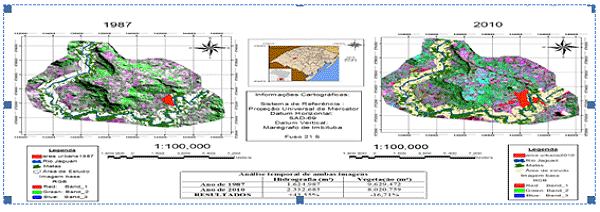
Figure I- Temporal analysis of the city of Jaguari – RS
Flows rates in southern Brazil show significant connections with the amount and distribution of rainfall, according to Silva, Lermen and Nery (2001); cold fronts in southern Brazil are mainly due to the El Niño Southern Oscillation (ENOS) through the warming that occurs in the waters of the Tropical Pacific Ocean, which result in changes in large-scale circulation of the atmosphere, this idea is also corrobored by Marengo (2008). Teixeira (2006) pointed out a rapid trend of rainfall events in southern Brazil and their main cause is El Niño.
As shown in Figure 2, periods of occurrence of affluence flows above average and decrease periods may be related to the seasonal effects of rainfall occurred during the period under study.
The descriptive statistics of the series under analysis showed a kurtosis higher than 3.46 and nonzero asymmetry, and it is possible to observe that the series does not follow a normal distribution and probably will present volatility characteristics, such as volatility grouping periods, known as clustering, according to Campos (2007); Ceretta et al. (2010).
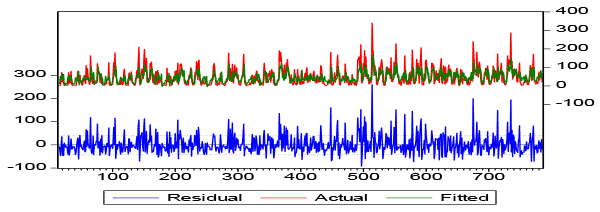
Figure II- (A) Flow Hydrograph
ARIMA and SARIMA general class filters have been used for modeling time series, according to Noakes, McLoad and Hipel (1985); Fill, Oliveira and Santos (2008); Andradóttir, Rueda, Armengol, Marcé (2012). By analyzing the autocorrelation function and the unit root tests, the historical affluence flow series is stationary at level I (0), showing a seasonal autocorrelation of 12 order. From this stage on, several linear filters were tested and the ARIMA seasonal filter showed to be the best filter able to capture the behavior of the average flow regime of the river Jaguari, represented by a SARIMA (1,0,1) (1,0,1)12, being considered the most parsimonious model when compared with other competing filters, as shown in equation 7.
(7)
The values ??in parentheses are corresponding to statistics, "t", calculated, where is possible to verify that all parameters are significant and modeling showed the white noise characteristic.
Aiming to analyze the flow series variability, the presence of volatility was tested by means of LM-ARCH test, in the quadratic residues of the linear model, where it showed that a p-value < 0.05 evidences that the conditional heteroscedasticity is present in the linear modeling residues, then equation (8) provides volatility estimate by means of ARCH modeling.
(8)
It is noticed that the parameter value shown by ARCH (1) volatility model is equal to 0.120633, which is relatively low and do not represent a lasting persisting, this idea is corrobored by Casarin et al. (2012), where is shown that an ARCH (1) parameter close to 1 shows to be persistent, that is the process variability should converge to the historical average, after a long period of time, affecting subsequent periods. Figure 3 shows the conditional volatility of the series under study.
Figure III- Conditional Standard Deviation
Figure 3 shows the intrinsic variability during the time series, showing periods of lower and higher variability amplitudes. It may be concluded that with a low parameter (0.12063) the affluence flow will not remain for a long period, thus converging to the historical average in a short time, where nature effects will directly influence oscillation.
4. Final Remarks
Results showed that it is possible by means of SARIMA (1,0,1) (1,0,1)12 - ARCH (1) filters represent the generating process series of the affluence flow of the Jaguari River, thus helping in the decision-making in hydroelectric sector and water resources management. It is observed that the ARIMA modeling was able to capture the effects of seasonality in this series and to understand the periods of higher and lower amplitude of the flows.
ARCH models also showed that although there is a volatility effect, it does not have a high persistence, which makes the variability period quickly returns to its usual variability level. According to Perrin et al (2003), the model structure and mathematical functions set applied are factors that should represent the behavior of the basin and the complexity level in the model structure to ensure the best result, thus stochastic models used methods prevail as able to understand the average level and the volatility of the time series flows.
It is also noticed that in addition to seasonal periods presented by the watershed, ARCH models were able to capture the periods of lowest and highest variability amplitudes, these periods that should serve as a warning for the future, because they are already being captured by probabilistic models employed. Although the effect is not lasting, a sign can be considered as an alert.
This research does not refers to the physical modeling in the study of the behavior of affluence flows approached by Formaggio, Campos and Amaral (2009), which showed that the soil texture, geomorphology, geology, hydrogeology and rainfall, respectively, are associated with the ease degree of water infiltration into the soil, causing the water variability water in free aquifers.
It is suggested for future research the employing of other methods to explain the behavior of the flows, as well as the inclusion of new variables to compose the study, in order to establish a dynamic system that represents the watershed as a whole, therefore establishing new practical results to the hydroelectrical sector.
5. Acknowledgements
The authors thank CAPES - Foundation, Brazilian Ministry of Education, the Laboratory of Statistical Analysis and Modeling - LAME - CCNE - UFSM and the anonymous reviewers for their contributions to the improvement of this study.
6. References
ANA. (2012) “Séries históricas”. Available in: < Link>. Access in 28 august 2012.
Andradottir, H. Ó., F. J. Rueda, J. Armengol, and R. marcé. (2012); “Characterization of residence time variability in a managed monomictic reservoir”. Water Resour. Res. doi: 10.1029/2012WR012069, in press. Available in: < Link>. Access in 08 september 2012.
Barros, N, G, F; Amin, M, M.(2008); “Água: Um bem econômico de valor para o Brasil e o mundo”. Rev. Brasileira de Gestão e Desenvolvimento Regional, v. 4, n. 1, p. 75-108, SP. Available in: < Link>. Access in 02 september 2012.
Box, G. E. P.; Jenkins, G. M. “Time Series Analysis:Forecasting and Control”. San Francisco: Holden-Day, 1970.
Britto, P, F; Barletta, R; Mendonça, M. (2008); “Variabilidade espacial e temporal da precipitação pluvial no Rio Grande do Sul: Influência do fenômeno El Niño Oscilação Sul”. Rev. Brasileira de Climatologia. Available in:<http://ojs.c3sl.ufpr.br/ojs2/index.php/revistaabclima/article/viewFile/25408/17040>. Access in 28 august 2012.
Campos, K. C. (2007); “Análise da volatilidade de preços de produtos agropecuários no Brasil”. Revista de Economia de Agronegócio. v. 5, n. 3. p. 303-328. Available in:< Link>. Access in 12 august 2012.
Casarin, A, V; Souza, M, A; Spim, A, J. (2012); “Continuons casting process stability evaluated by means of residuals control charts in the presence of cross-Correlation and autocorrelation”. International Journal of Academic Research, Vol.4. No.3. Available in:< Link>. Access in 27 september 2012.
Ceretta, S, P; Barba, G, F; Vieira, M, K; Casarin, F. (2011); “Previsão da volatilidade Intradiária: Análise das distribuições alternativas”. Rev. Bras. Finanças, Rio de Janeiro, Vol. 9, No. 2, pp. 209–226. Available in: < Link>. Access in 29 august 2012.
Cervilha, B, G; Filho, S, C, A. (2011); “Métodos estocásticos e não-estocásticos para a previsão da vazão em rios”. II Congresso de iniciação cientifica. Available in: < Link>. Access in 29 july 2011.
Costa, S, F; Maceira, P, E, M; Damázio, M, J. (2007); “Modelos de previsão hidrológica aplicados ao planejamento da operação do sistema elétrico Brasileiro”. Rev. Brasileira de Recursos Hídricos, Vol. 12 n.3. Available in: < Link>. Access in 29 august 2012.
Engle, R. F. (1982); “Autoregressive Conditional heteroscedasticity with estimates of the variance of U.K. inflation”. Econometrica. 50: 987-1008.
Fadiga, M, F; Lopes, G, E, J; Martins, S, R, J; Barros, L, T, M; Santos, P, C, R. (2007); “Modelos de previsão de vazões para a bacia incremental à UHE Itaipu”. Revista Brasileira de Recursos Hídricos, Vol. 12 n.3. Available in:<Link>. Access in 29 august 2012.
Fill, D, H; Oliveira, B, F; Santos, P. (2008); “Avaliação de cheias considerando distribuições sazonais”. Rev. Brasileira de Recursos Hídricos.Vol. 13 n.2, p.5-13. Available in: < Link>. Acess in 4 september 2012.
Fuller, D, A. W.A. (1981); “Likelihood ratio statistics for autoregressive time series with a unit root”.Econometrica, 49:1057-1072.
Gomes, A, M; Lani, L, J; Costa, M, L; Pontes, M, L; Figueredo, A, N; Bardales, G, N. (2012); “Solos, manejo e aspectos hidrológicos na bacia hidrográfica do Araújos, Viçosa – MG” Revista Árvore vol.36 no.1 Viçosa. Available in: < Link>. Access in 31 august 2012.
Güldal, V; Tongal, H. (2010); “Comparison of Recurrent Neural Network, Adaptive Neuro-Fuzzy Inference System and Stochastic Models in E
Guo, S. (1995); “Impact of climatic change on hydrological balance and water resource systems in the Dongjiang Basin, China: Modeling and Management of Sustainable Basin-Scale”. Water Resource. Proceedings of a Boulder Symposium, LAHS Publication, n. 231. Available in: < http://iahs.info/redbooks/a231/iahs_231_0141.pdf>. Access in 4 september 2012.
IEA International Energy Agency. (2010); “Perspectivas em Tecnologias Energéticas. 2010”. Available in: <http://www.iea.org/techno/etp/etp10/PortugueseExecutiveSummary.pdf>. Access in 29 august 2012.
Kwiatkowski, D, P.C.B. Phillips, P. Schmidt, Y. Shin. (1992); “Testing the Null Hypothesis of Stationarity against the Alternative of a Unit Root”. Journal of Econometrics, 54, pp. 159-178, North-Holland.
Lienert, M; Lochner, S. (2012); “The importance of market interdependencies in modeling energy systems-The case of the European electricity generation market”. International Journal of Electrical Power & Energy Systems, Vol. 34, Issue 1, Pages 99-113. Available in: <Link>. Access in 04 september 2012.
Lucas, M, W, E; Sousa, S, A, F; Silva, S, D, F; Lucio, S, P. (2009); “Modelagem hidrológica determinística e estocástica aplicada à região hidrográfica do Xingu – Pará”. Rev. Brasileira de Meteorologia, v.24, n.3, pp 308-322. Available in:< Link>. Access in 01 september 2012.
Marchezan, A; Souza, M, A. (2010); “Previsão do preço dos principais grãos produzidos no Rio Grande do Sul”. Cienc. Rural vol.40 no.11 Santa Maria. Available in: < Link>. Access in 03 september 2012.
Marengo, A, J. (2008); “Água e mudanças climáticas”. Rev. Estudos Avançados, vol.22 no. 63. São Paulo. Available in: < Link>. Access in 02 september 2012.
Morettin, P. A. (2006); “Econometria financeira:Um curso em séries temporais financeiras”. 17º Simpósio Nacional de Probabilidade e Estatística. ABE. Caxambu.
Noakes, J, D; Mcleod, A; Hipel, W, K. (1985); “Forecasting monthly river flow time series”. International Journal of Forecasting, Volume 1, Issue 2, Pages 179-190. Available in: <link>. Access in 04 de september 2012.
ONS- “Operador nacional do sistema elétrico”. (2012). Available in: < >Link>. Access in 05 july 2012.
Prina, Z, B; Monguilhot, M. (2011); “Análise das transformações da paisagem de áreas próximas ao rio Jaguari aplicando técnicas de sensoriamento remoto em imagens do satélite TM Landsat-5”. XV Simpósio Brasileiro de Sensoriamento Remoto - SBSR, Curitiba, PR, Brasil, INPE p.3812. Available in: < http://www.dsr.inpe.br/sbsr2011/files/p1036.pdf>. Acess in 31 august 2012.
Righi, E; Robaina, S, E, L. (2008); “Estudos Geoambientais: Mapeamento de bacias hidrográficas no oeste do Rio Grande do Sul”. Rev. Geografia, V. 17, n.1. Available in:< Link>. Access in 01 september 2012.
Rodrigues, L, S, A; Malafaia, G; Castro, A, T, P. (2010); “A importância da avaliação do habitat no monitoramento da qualidade dos recursos hídricos: Uma revisão”. Rev. Saúde e Biol, v. 5, n. 1, p. 26-42. Available in:< Link>. Access in 24 august 2012.
Silva, J, É; Jabbour, C, J, C. (2012); “Gestão para eficiência energética: Levantamento e análise da produção científica divulgada em alguns periódicos das áreas de engenharia de produção e administração (2001-2011)”. Espacios. Vol. 33 (5). Pág. 5. Available in: < Link>. Access in: 15 september 2012.
Souza, M, A; Souza, M, F; Menezes. R. (2012); “Procedure to Evaluate Multivariate Statistical Process Control using ARIMA-ARCH Models”. Japan Industrial Management Association. Vol.63.No. 2E. Available in: < Link>. Access in: 24 august 2012.
Teixeira, S, M. (2006); “Dynamical and synoptic characteristics of heavy rainfall episodes in Southern Brazil”. Mon Wea Rev., n.135, p.598-617. Available in: <Link>. Access in 31 august 2012.
Tucci, C, E, M.(1998); “Modelos Hidrológicos”. Editora Universitária UFRGS - Porto Alegre.
Vicini, L. e Souza, A. M. (2007); “Geração de subsídios para a tomada de decisão na cadeia produtiva da bovinocultura do Brasil”. Gestão de Produção, Operações e Sistemas, 4, 49-64. Available in:< Link>. Access in: 28 september 2012.
Jacobs, W; Costa, M. (2011); “Previsão da demanda de um produto industrial utilizando a metodologia de Box-Jenkins”. Rev. Destaques Acadêmicos, ano 3, n. 4, cetec/univates. Available in:<Link>. Access in 03 september 2012.
Xiong, L; Guo, S, A. (1999); “A two-parameter monthly water balance model and its application”. Journal of hydrology, V.216, n.1, p.111-123. Available in: < Link>. Access in 04 september 2012.
Yilmaz, B and Harmancioglu, NB. (2010); “Multi-criteria decision making for water resource management: a case study of the Gediz River basin, Turkey”. Water SA (Online). vol.36, n.5, pp. 563-576. Available in: < Link>. Access in 12 august 2012.