1. Introdução
Para Nakajima (1988) o indicador de Índice do Rendimento Operacional Global (IROG) deve ser considerado como um indicador operacional e pode ser aplicado em diversos níveis dentro de um sistema de manufatura. Num primeiro momento o IROG pode ser usado como benchmarking para medir o nível de desempenho de um sistema produtivo de forma global. Ou seja, o IROG é medido inicialmente e comparado com um IROG futuro após o sistema ter passado por um programa de melhorias ou então comparado com o desempenho de outros sistemas semelhantes.
O IROG também pode ser calculado em sistemas de manufatura com diversas linhas de produção, proporcionando verificar quais os reais níveis de utilização dos ativos da indústria (Muthiah e Huang, 2007; Muthiah et al., 2008; Garza-Reyes et al., 2010). Outra perspectiva de adoção do cálculo do IROG é no contexto de equipamentos individuais. Nesse caso de aplicação o IROG resulta em uma métrica quantitativa de produtividade que possibilita identificar quais equipamentos possuem desempenho alto ou baixo em relação a uma dada meta. Sendo considerado assim, como um relevante elemento dentro da abordagem da Total Productive Maintenance (Braglia et al., 2008; Mathur et al., 2011; Muthiah e Huang, 2007).
De forma geral, tal indicador é importante porque permite mensurar a real capacidade produtiva dos equipamentos para um período de tempo pré-determinado ou demanda conhecida. Nesse sentido, torna-se relevante explorar o conceito do IROG para a discussão da capacidade tanto de equipamentos, de forma específica, como de sistemas produtivos complexos, de forma mais ampla. Os estudos de Wakjira e Singh (2012) e Ahuja e Khamba (2008), por exemplo, evidenciaram em suas pesquisas a melhoria de desempenho operacional que a organização como um todo pode obter após a aplicação integral ou parcial da TPM.
Por outro lado, a Teoria das Restrições criada por Goldratt (1984) propõe uma metodologia para identificar a restrição de capacidade que define o desempenho global do sistema produtivo e, a partir daí, explorá-la a fim de elevar a capacidade instalada e o ganho global desse sistema. A restrição de capacidade é o gargalo do sistema, que é definido como sendo o recurso cuja capacidade disponível é menor do que a capacidade necessária para atender a demanda imposta a ele, num determinado período de tempo, o qual é geralmente longo (Antunes, 1998). O método Tambor-Pulmão-Corda é o algoritmo usado para explorar a capacidade do gargalo e será posteriormente detalhado nesse estudo.
Nesse sentido, é possível perceber um certo grau de convergência entre os temas em discussão nesse artigo. Ou seja, por um lado, tem-se o IROG que sobretudo permite: i) avaliar se o desempenho do sistema produtivo é alto ou baixo, ao medir o nível de desempenho de forma global; ii) avaliar se o desempenho de um dado equipamento é alto ou baixo, medindo-o isoladamente, e; iii) verificar quais os reais níveis de utilização dos ativos. De maneira complementar, a TOC identifica a restrição de capacidade que define o desempenho global do sistema produtivo e a explora a fim de elevar a capacidade global. Parece ser possível então concluir que as duas abordagens podem ser integradas, visando a melhor gestão da capacidade dos sistemas produtivos à luz da Engenharia de Produção e da Gestão de Operações.
Assim sendo, esse artigo discute e apresenta um modelo de gerenciamento da capacidade produtiva em sistemas produtivos integrando os conceitos da Teoria das Restrições e da Total Productive Maintenance (TPM). O objetivo do presente trabalho é discutir e sugerir um modelo de gerenciamento da capacidade, capaz de responder às seguintes questões centrais: i) quais indicadores de capacidade devem ser considerados e como medi-los para mensurar a capacidade de sistemas de manufatura? ii) qual é a real capacidade do sistema produtivo em análise frente a uma determinada relação entre capacidade e demanda do mercado. Para atender a tal propósito esse artigo esta estruturado da seguinte maneira: as seções 2, 3 e 4 apresentam objetivamente a revisão da literatura sobre capacidade produtiva, TPM, IROG e Teoria das Restrições; a seção 5 apresenta e descreve as etapas do modelo proposto; e a seção 6 descreve as conclusões e as sugestões para trabalhos futuros.
2. Capacidade produtiva na manufatura
Hayes et al. (2008) argumentam que medir a capacidade de sistemas produtivos é uma tarefa complexa, devido à ação dos seguintes fatores associados à variabilidade: políticas da empresa, confiabilidade dos fornecedores, confiabilidade dos equipamentos, taxas de produção e o impacto dos fatores humanos. Para Hopp e Spearman (2001) a variabilidade existe em todos os sistemas de produção e pode causar um grande impacto no seu desempenho. Por esta razão, a habilidade de medir, compreender e gerenciá-la torna-se crítica para uma administração eficaz da produção.
Hopp e Spearman (2001) também apresentaram os seguintes pressupostos sobre o gerenciamento da capacidade produtiva em sistemas: i) uma linha de fluxo desequilibrada com um gargalo conhecido é mais fácil de administrar e demonstra um comportamento logístico melhor quando comparado com uma linha em equilíbrio, onde os tempos de processamento das operações são semelhantes; ii) a capacidade está geralmente disponível apenas em tamanhos incrementais pré-determinados, ou seja, podemos comprar um ou dois recursos, mas não um e meio e pode ser impossível ajustar idealmente a capacidade de determinada operação com a meta de produção; iii) o custo da capacidade, geralmente, não é o mesmo em cada estação de trabalho e é mais barato manter capacidade em excesso em algumas estações do que em outras.
Avançando na discussão sobre capacidade, segundo Antunes et al. (2008) a capacidade e a demanda de um dado recurso, em unidades de tempo, podem ser determinadas respectivamente, de acordo com as Equações 1 e 2 a seguir:
![]() [1]
[1]
Onde:
C: Capacidade de produção para a produção; Tt: Tempo total disponível para a produção (tempo); μg: Índice de Rendimento Operacional Global do equipamento (IROG). Já a demanda, em unidades de tempo, de um dado recurso pode ser calculada de acordo com o que determina a Equação 2.
![]() [2]
[2]
Onde:
D: Demanda de produtos no equipamento (tempo); Tpi: Taxa de processamento da peça i no equipamento (tempo por unidade de produção); qi: Quantidade produzida da peça i no equipamento (unidades de produção).
3. Total Productive Maintenance (TPM) e o Índice de Rendimento Operacional Global (IROG)
O conceito de eficiência dos equipamentos e o termo IROG foram apresentados por Nakajima (1988). Sua discussão é central para o cálculo da capacidade porque determina, a priori, a capacidade prática e não teórica dos equipamentos e sistemas. A Equação 3 apresenta a equação genérica de cálculo do IROG:
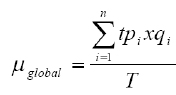 [3]
[3]
Onde:
μg: Índice de Rendimento Operacional Global do equipamento (IROG); tp: é o tempo de ciclo ou tempo padrão do produto X; q: é a quantidade de produtos X processados; T: é o tempo disponível para a produção.
Verifica-se nesta equação, que a multiplicação do tempo de ciclo de um produto pela quantidade produzida deste produto em um determinado equipamento corresponde ao tempo de agregação de valor deste equipamento no processo de produção sobre o prisma das práticas enxutas (Antunes, 1998). Ou seja, trata-se do tempo em que o equipamento efetivamente funcionou adicionando valor ao produto. O tempo de ciclo é o tempo que um operador devidamente treinado processa uma peça em um equipamento específico, de forma a realizá-la normalmente. Isto é, sem realizar esta atividade velozmente, de maneira a não conseguir manter o mesmo ritmo durante o seu período de trabalho, e sem realizá-la de forma muito lenta, como ocorre normalmente quando um operador se encontra em fase de treinamento ou não está familiarizado com a operação. Apesar de ser considerado um medidor otimizado, o IROG indica qual é a direção para a realização de melhorias no equipamento ou então do sistema produtivo em análise (Braglia et al., 2008; Mathur et al., 2001). O cálculo do IROG, segundo Antunes et al. (2008), também pode ser feito considerando os seguintes aspectos:
a) Se o posto de trabalho é um recurso gargalo: neste caso, o indicador IROG é denominado de TEEP, ou seja, Produtividade Efetiva Total do Equipamento (Total Effective Equipment Productivity). Nesse caso, o tempo T considerado na equação 3 é o tempo total – no caso dos recursos críticos gargalos, 24 horas/dia (Mathur et al., 2011). Isto se explica pelo fato de que, sendo o posto de trabalho um gargalo, todo o tempo disponível deve ser utilizado na produção. Este índice indica o tempo que pode ser ganho para produzir e corresponde à produtividade real do sistema produtivo a partir da capacidade do gargalo.
b) Se o posto de trabalho é um recurso não gargalo: neste caso, o indicador IROG é denominado de OEE, ou seja, Índice de Eficiência Global (Overall Equipment Efficiency). O tempo T considerado na equação 3 é o tempo disponível, obtido pela diferença entre o tempo total e o tempo das paradas programadas. Por não se tratar de um posto de trabalho gargalo, é possível programar certas paradas como: parada para almoço, ginástica laboral, etc., uma vez que a não paralisação deste equipamento geraria estoques intermediários antes do gargalo. Este índice indica a eficácia do equipamento durante o tempo de operação programado.
As considerações acima consistem no cálculo da eficiência global dos equipamentos através da equação geral, devendo ser desdobradas, segundo Nakajima (1988) com a finalidade de identificar as principais causas das ineficiências observadas no posto de trabalho. O cálculo da eficiência global é então definido pelos seguintes índices de eficiência, conforme a Equação 4 que são descritos a seguir:
![]() [4]
[4]
Onde:
μ1: Índice de Tempo Operacional – ITO;
μ2: Índice de Performance Operacional – IPO;
μ3: Índice de Produtos Aprovados – IPA.
O indicador ITO corresponde ao tempo em que o equipamento ficou disponível, excluindo-se as paradas não programadas. É relacionado, portanto, com a paralisação do equipamento. Isto é, quando a velocidade do mesmo cai para zero como no caso de quebras, trocas de ferramentas e ajustes (Mathur et al., 2011; Muthiah e Huang, 2007). Quanto menor for o valor do ITO, maior será o potencial de aumento da utilização do posto de trabalho. Isso ocorre porque um baixo valor indica que o equipamento sofre muitas paradas não programadas. E os recursos que processam pouca variedade de peças, tendem a ter um ITO elevado devido à baixa necessidade de trocas de ferramentas, preparações e ajustes.
O IPO mede o desempenho operacional do recurso, sendo calculado em função do tempo disponível e à redução da velocidade do mesmo, operação em vazio e paradas momentâneas (Muthiah e Huang, 2007). É relacionado, portanto, com a queda de velocidade do recurso (velocidade diferente da nominal e diferente de zero). As causas que geram valor baixo do IPO podem ser: i) do tipo técnicas, como operações em vazio por falta de alimentação de peças (não havendo assim agregação de valor) ou tempo de ciclo alto com a consequente redução da velocidade do processamento; ii) de rotina, como o não registro dos dados no diário de bordo ou sistema de coleta (por exemplo, paradas pequenas e sucessivas, onde o somatório tem impacto significativo no valor final do IPO). O último indicador analisado é o IPA que mede a qualidade das peças produzidas, sendo calculado em função do tempo de operação real, excluindo-se o tempo gasto com refugos ou retrabalhos (Mathur et al., 2011; Muthiah et al., 2008).
A literatura evidencia que após o surgimento do IROG a partir da obra de Nakajima (1988), surgiram outros medidores, os quais derivam essencialmente do IROG. Nesse caso, é relevante para esse trabalho citar o OFE (Overall Factory Effectiveness) e o OTE (OverallThroughput Effectiveness), que foram elaborados para avaliar o desempenho de sistemas ou subsistemas inteiros (Muthiah et al., 2008; Muthiah e Huang, 2007; Mathur et al., 2011). Uma perspectiva mais ampla de implantação e desdobramentos de tais indicadores pode ser encontrada em Scott e Pisa (1998), Muthiah et al. (2008) e em Muthiahe Huang (2007).
É importante também salientar que a discussão integrando TPM, IROG e a TOC, foi sugerida e analisada na literatura por alguns autores (Jeong e Phillips, 2001; Rose et al.,1995; Chakravorty e Atwater, 2006). A discussão proposta por tais autores corrobora com os esforços de pesquisa do modelo alternativo proposto no presente trabalho. Conforme Jeong e Phillips (2001), por exemplo, a TPM enfatiza a manutenção autônoma e os recursos gargalos deveriam ter maior prioridade em detrimento dos recursos não gargalos dos sistemas produtivos. O IROG segundo Rose et al.(1995), quando aplicado ao recurso gargalo, pode aumentar o ganho do sistema. Portanto, medir a eficiência e a previsibilidade das eficiências do recurso gargalo do sistema produtivo é fundamental para o gerenciamento de tal sistema (Agi, 2010). Ronen e Pass (2010), corroboram com esta afirmação enfatizando que devem ser prioritárias as atividades que resultarão em maior ganho para a organização. Sendo assim, de forma geral, pode-se concluir que o gerenciamento de gargalos sugerido pela TOC, somando-se ao indicador IROG oriundo da abordagem da TPM, podem contribuir não só para efetivo aumento da produtividade, como também para elevar o ganho de sistemas produtivos.
4. Teoria das Restrições
Segundo Cox e Spencer (2002) a Teoria das Restrições pode ser entendida a partir dos seus seguintes componentes:
a) Uma abordagem Logística e de Operações, que envolve os seguintes métodos: i) Os cinco passos envolvendo o foco na melhoria dos processos; ii) O processo de programação da produção envolvendo o gerenciamento via a lógica TPC (Tambor, Pulmão e Corda) e o gerenciamento dos pulmões no sistema produtivo; iii) A análise dos sistemas produtivos adotando a classificação V-A-T.
b) A proposição de um Sistema de Indicadores de Desempenho, que passa pela: i) Definição dos Ganhos, Inventários e Despesas Operacionais da Empresa; ii) Definição do mix de produtos que deverá ser produzido visando maximizar os resultados; iii) A lógica dos Ganhos por dia e dos Inventários por dia.
c) E por fim, a TOC pode ser entendida como um Processo de Pensamento visando à solução de problemas, que envolve as seguintes técnicas: i) Os diagramas de efeito-causa-efeito, que são: a Árvore da Realidade Atual, Árvore da Realidade Futura, Árvore dos Pré-Requisitos e Árvore de Transição; ii) O método da Evaporação das Nuvens.
Os cinco passos de melhoria contínua dos processos da TOC podem ser aplicados para o gerenciamento do gargalo do sistema. Por isso o detalhamento desse método é relevante na discussão dessa pesquisa sobre gerenciamento da capacidade produtiva. De forma objetiva, os cinco passos da TOC para melhoria de processos segundo Goldratt (1996) são:
1. Identificar a(s) restrição(ões) do sistema: elas podem ser internas ou externas à empresa. Quando a demanda total de um dado mix de produtos é maior do que a capacidade da fábrica se diz que existe um gargalo de produção. Todavia, quando a capacidade de produção é superior à demanda de produção, a restrição é externa ao sistema.
2. Explorar da melhor forma possível a(s) restrição(ões) do sistema: se a restrição é interna à fábrica, a melhor decisão consiste em maximizar o ganho no(s) gargalo(s), fazendo que o maior número possível de produtos pré-definidos pelo critério de maior geração de ganho, passem pelo gargalo.
3. Subordinar todos os demais recursos à decisão tomada no passo 2: a lógica deste passo, independentemente da restrição ser externa ou interna, consiste em reduzir ao máximo os inventários e as despesas operacionais e ao mesmo tempo garantir o ganho teórico máximo do sistema de produção.
4. Elevar a capacidade da(s) restrição(ões): se o gargalo for interno é necessário aumentar sua capacidade produtiva. Isso pode ser feito através de mudanças de leiaute, compra de equipamentos, uso de horas extras, redução da variabilidade, redução de setup, aplicação das técnicas da manufatura enxuta, etc.
5. Voltar ao passo 1 para não deixar que a inércia tome conta do sistema: ao elevar a capacidade produtiva da restrição o sistema torna-se, a priori, um sistema genérico, o que gera a necessidade de analisá-lo novamente. O passo cinco retoma a ideia de melhoria contínua dos processos.
4.1 O algoritmo Tambor-Pulmão-Corda (TPC) e o aumento da capacidade
Para Goldratt (1996) o TPC visa operacionalizar no chão de fábrica os cinco passos de melhoria dos processos da TOC. A lógica central do algoritmo TPC consiste em estabelecer a produção puxada para controlar o fluxo de inventário no sistema produtivo (Watson e Patty, 2009). Tanto os cinco passos de melhoria de processos da TOC, já supracitados, quanto o TPC, estão inseridos no modelo discutido nesse trabalho. Assim sendo, de forma objetiva os elementos da lógica TPC serão descritos a seguir e estão representados no esquema da Figura 1:
- Tambor (T): é o gargalo do sistema, o qual determina sua capacidade produtiva total (Watson e Patty, 2009; Umble e Umble, 1999). Portanto, define o ritmo da produção e restringe a capacidade, ou seja, é o Tambor do sistema, uma vez que dita o seu ritmo de produção (Dettmer, 2001; Rahman, 1998).
- Pulmão (P): é a proteção colocada antes do tambor para evitar interrupções no tambor devido ao impacto das variabilidades, como quebra de máquinas, variação no tempo de processo, problemas de qualidade, falta de matéria prima para produzir, etc. Em outras palavras, pulmão é um elemento estratégico que busca proteger o ganho do sistema sobre as variações do mesmo (Watson e Patty, 2009; Rahman, 1998). Há três tipos de pulmão que podem ser usados nesse caso: pulmão de tempo, inventário ou pulmão de capacidade.
- Corda (C): tem o objetivo de sinalizar a necessidade de entrada de materiais no sistema, para alimentar o pulmão e o gargalo, limitando a quantidade de matéria-prima liberada para a fábrica. Assim sendo, a função da corda, que pode ser um fluxo físico ou de informação, é liberar os materiais em função do consumo de materiais do gargalo (Watson e Patty, 2009).
Figura 1 – Algoritmo TPC. Fonte: Antunes (1998).
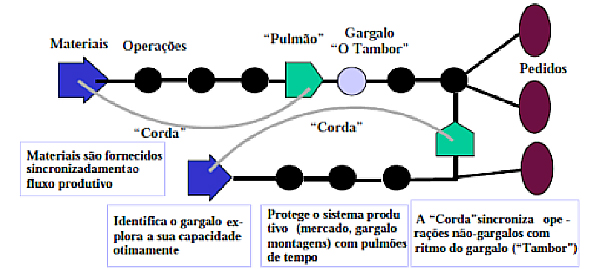
O algoritmo TPC sincroniza a utilização dos recursos e materiais, os quais são usados apenas em um determinado nível para a geração de ganho no processo (Umble e Umble, 1999; Rahamn, 1998). As vantagens de uso do TPC são corroboradas com a evidência de resultados de implantações presentes na literatura (Goldratt, 2009). A pesquisa de Mabin e Baderstorne (2003) evidenciou estes benefícios a partir da melhoria de desempenho no lead time, nos tempo de ciclo e na ampliação das receitas, ou ganho na lógica da TOC, de organizações que aplicaram o TPC. Corroborando com estas evidências, Patty e Watson (2008) concluíram que empresas que utilizam TPC alcançam maiores ganhos gerando menos estoques. Na mesma linha de discussão, Ifandoudas e Chapman (2009) afirmam que este processo busca determinar o que, quando e como a produção será coordenada de forma a reduzir inventário e maximizar as vendas. Sendo assim, o TPC é um algoritmo que objetiva, por meio dos cinco passos de focalização da TOC, coordenar sistemas produtivos (Gupta e Boyd, 2008). Sendo assim, considerando as contribuições da TOC, pode-se afirmar que as organizações são sistemas que devem gerar ganho em função de uma restrição inerente a tal sistema (Walsh, 2010). Logo, se primeiramente monitorarmos tal restrição e posteriormente executarmos atividades voltadas para o aumento da eficiência da restrição, através da utilização de IROG, estaremos caminhando em direção a maximização do ganho do sistema, ou seja, maximizando o ganho da organização.
5. Modelo de gerenciamento da capacidade produtiva
O modelo proposto nessa pesquisa possui alguns pressupostos considerados no desenvolvimento do método, os quais devem ser avaliados na sua aplicação empírica. Em primeiro lugar, o modelo considera que a restrição da empresa é interna ao sistema produtivo, podendo ser um recurso físico, equipamento, linha de produção, célula, etc. Outro pressuposto do modelo é que a variedade de produtos fabricados em qualquer recurso do sistema não impacta nos resultados apresentados. Ou seja, o método pode ser aplicado em ambientes de manufatura de alto ou baixo nível de customização dos produtos fabricados.
O modelo também se adapta tanto para sistemas de manufatura de produção puxada quanto para ambientes sob a lógica empurrada. Um aspecto positivo do modelo é que o tamanho do período de tempo em análise não influencia no modelo. Pode-se analisar um dia, um mês, um ano e assim por diante. Um aspecto fundamental a considerar antes de se aplicar o método é que as informações de entrada como: quantidades demandadas e principalmente os tempos de processamento sejam confiáveis. Esse aspecto relacionado com a acuracidade das informações é um pré-requisito para se definir com precisão qual recurso é a restrição do sistema. Será analisado a seguir um caso teórico em uma linha de produção composta de cinco recursos onde são manufaturados um tipo de produto, denominado de X, composto de dois componentes (A e B). O modelo proposto é composto pelas seguintes etapas, conforme Figura 2:
Figura 2 – Etapas do modelo de gerenciamento da capacidade produtiva integrando TOC e TPM.

Fonte: elaborado pelos autores (2012).
A seguir, serão apresentadas e descritas as etapas do modelo proposto na Figura 2 que está em debate no presente estudo:
- Identificar a restrição do sistema: nessa etapa do modelo é identificada a restrição do sistema, cuja capacidade é inferior à demanda imposta, a partir das análises do passo 1 da TOC. Nesse caso, a análise baseou-se na abordagem de Capacidade x Demanda proposta por Antunes et al. (2008) e fez a proposição de algumas alterações nesse método de análise dos autores, visando seu aperfeiçoamento. As alterações sugeridas de forma a aperfeiçoar o modelo de Capacidade x Demanda proposto por Antunes et al. (2008) podem ser evidenciadas ao se comparar a Tabela 1, que traz valores hipotéticos, com os novos indicadores IPAC e o IROGC propostos na Tabela 2.
Tabela 1 – Método de Capacidade x Demanda. Fonte: Antunes et al. (2008).

Tabela 2 – Novos indicadores propostos para o método de Capacidade x Demanda. Fonte: elaborado pelos autores (2012).

- Explorar a restrição: nessa etapa o gargalo do sistema é explorado visando maximizar o ganho do sistema, porém, sem investimentos adicionais, conforme preconiza o passo 2 do processo de focalização da TOC.
- Subordinar os demais recursos à restrição: nessa etapa os recursos que estão dispostos no leiaute do sistema produtivo, tanto à jusante quanto à montante do gargalo, são subordinados ao gargalo, de acordo com o passo 3 da TOC. O objetivo dessa etapa do modelo é assegurar que a capacidade do gargalo irá definir o planejamento e controle da produção no sistema produtivo.
- Definir o IROG (Índice de Rendimento Operacional Global) da restrição: nessa etapa do modelo calcula-se o TEEP do gargalo conforme apresentado e discutido previamente na seção 3. O objetivo principal dessa etapa é avaliar o nível atual de desempenho do recurso gargalo do sistema.
- Definir o novo Índice de Produtos Aprovados Corrigido (IPAC) do sistema: nessa etapa do modelo, calcula-se o IPA de todos os recursos dispostos no fluxo de produção após o gargalo e efetua-se a multiplicação entre esses índices calculados, obtendo-se assim um valor único, denominado de IPA Corrigido (IPAC). Ao mensurar a quantidade de produtos rejeitados no fluxo após o gargalo, é possível medir o real índice de produtos conformes quanto à qualidade, que são produzidos após o gargalo contribuindo para um dimensionamento mais acurado da capacidade global de saída do sistema. Esse aspecto do modelo, é uma das principais lacunas que o presente estudo pretende preencher dentre os modelos de gerenciamento de capacidade até então apresentados no campo da Engenharia de Produção e da Gestão de Operações.
- Definir o IROG Corrigido do sistema (Índice de Rendimento Operacional Global Corrigido): nessa etapa do modelo é obtido o novo IROG do sistema, a partir da visão de capacidade dos gargalos da TOC, denominado nesse estudo de IROGC. O resultado é obtido multiplicando-se o IROG calculado na etapa 4 pelo indicador IPAC obtido na etapa 5.
- Definir a capacidade real do sistema: nessa etapa do modelo define-se a capacidade real do sistema em atender à demanda a partir da capacidade do gargalo. O resultado é obtido multiplicando-se o tempo disponível para a produção no recurso gargalo pelo valor do IROGC obtido na etapa 6. Dessa maneira, a partir da análise da diferença temporal resultante da análise, é possível avaliar se o sistema possui capacidade ou não de atender à demanda imposta que está sendo analisada nos recursos.
- Calcular a quantidade teórica de produtos não atendidos pelo sistema: essa etapa do modelo consiste em dividir a diferença temporal do gargalo pelo somatório dos tempos de processamento do produto no recurso gargalo. Para fins de tomada de decisão gerencial, sugere-se que o resultado obtido seja arredondado para cima para minimizar o efeito de adição incremental da capacidade, conforme argumentam Hopp e Spearman (2001) e Umble e Srikanth (1995). O valor então obtido é a quantidade de produtos não atendida pelo sistema. O resultado é dito como teórico porque está relacionado diretamente com a confiabilidade dos dados de entrada de cálculo nos passos anteriores do modelo. Logo, nessa etapa do modelo se evidencia a importância de se ter uma base de dados confiável para as análises dos resultados apresentados pelo modelo. Além disso, se define como uma quantidade teórica porque é praticamente inviável prever com precisão o comportamento futuro de um sistema devido ao efeito das variabilidades dos processos produtivos (Hopp e Spearman, 2001). Assim sendo, caso depois de realizadas as etapas anteriores, seja verificado que há recursos com diferença temporal negativa, deve-se calcular novamente a quantidade teórica de produtos não atendida. Nesse caso, a quantidade de produtos não entregues pelo sistema, será o somatório da quantidade de produtos não entregues em todos os equipamentos cuja diferença temporal é negativa.
- Elevar a capacidade do gargalo: nessa etapa são realizadas ações, caso sejam necessárias, para elevar a capacidade do gargalo de acordo com o passo 4 da TOC. Nesse ínterim, diversas estratégias gerenciais podem ser adotadas, tais como: aplicar as técnicas enxutas de redução de perdas, reduzindo a variabilidade, reduzindo os tempos de setup, adquirindo outros recursos, usando horas extras, contratação de novos trabalhadores, usar roteiros alternativos reduzindo o tempo de operação dos produtos no gargalo, e assim por diante.
- Voltar à etapa 1: a lógica dessa etapa do modelo consiste em reavaliá-lo, aplicado o sentido de melhoria contínua de processos. Pretende-se nessa etapa, à luz da TOC, evitar que a inércia tome conta do sistema produtivo, de acordo como passo 5 da TOC.
6. Conclusões
O presente artigo apresentou um modelo de gerenciamento da capacidade em sistemas produtivos integrando os conceitos da Teoria das Restrições com uma abordagem para o uso do IROG do TPM diferente da que consta na tradicional literatura. O estudo apresentou quais indicadores de capacidade devem ser considerados e como medi-los para mensurar a real capacidade de sistemas de manufatura. O presente estudo também sugeriu um modelo dividido em etapas, as quais cada etapa é pré-requisito para as demais, para dimensionar a real capacidade de um sistema produtivo frente a uma determinada relação entre capacidade e demanda.
Nesse sentido, acredita-se que estudo atendeu ao primeiro objetivo proposto nessa pesquisa ao explicitar a real capacidade de um sistema produtivo. Da mesma maneira, pode-se dizer que a presente pesquisa também atendeu ao segundo objetivo proposto ao apresentar novos indicadores (IPAC e IROGC) que devem ser considerados na gestão da capacidade produtiva e ao descrever a maneira sugerida de calculá-los.
O modelo proposto é então apresentado como uma abordagem que não apenas contribui com o processo de tomada de decisão sobre os níveis de capacidade em sistemas produtivos, como também possibilita o melhor gerenciamento dos recursos e suas capacidades, da programação da produção no chão de fábrica e do atendimento às demandas programadas em ambientes da manufatura. Como extensão natural dessa pesquisa, sugere-se a aplicação de estudos de casos reais em empresas de diferentes segmentos de atuação, a fim de avaliar a abrangência de aplicação do modelo proposto, bem como a análise de outros elementos que possam ser inseridos no modelo proposto visando aperfeiçoa-lo.
Referências
AGI Goldratt Institute. (2010); Combining Lean, Six Sigma and the Theory of Constraints to Achieve Breakthrough Performance in The Theory of Constraints Handbook, 1st Edition, Cox III, J.F. & Schleier, J.G., (Eds), McGraw-Hill, New York.
Ahuja, I.P.S.; Khamba, J.S. (2008); Total productive maintenance – literature review and directions, International Journal of Quality & Reliability Management, Vol. 25 No. 7, pp. 709-56.
Antunes Jr., J.A.V. (1998); Em direção a uma teoria geral do processo na administração da produção: uma discussão sobre a possibilidade de unificação da teoria das restrições e a teoria que sustenta a construção dos sistemas de produção com estoque zero. Tese (doutorado em Administração de Empresas). Programa de Pós-Graduação em Administração da UFRGS, Porto Alegre, RS.
Antunes, J.; Alvarez, R.; Klippel, M.; Bortolotto, P.; De Pellegrin, I. (2008); Sistemas de Produção – Sistemas e Práticas para Projeto e Gestão da Produção Enxuta. Porto Alegre: Bookman.
Braglia, M.; Frosolini, M.; Zammori, F. (2008); Overall equipment effectiveness of a manufacturing line (OEEML): An integrated approach to assess systems performance, Journal of Manufacturing Technology Management, Vol. 20 Iss: 1 pp. 8 – 29.
Chakravorty, S.; Atwater, J. B. (2006); Bottleneck management: theory and practice.Production, Planning & Control, v. 17, n. 5, p. 441-447.
Cox, J.; Spencer, M. (2002); Manual da Teoria das Restrições. Porto Alegre: Bookman.
Dettmer, H. W. (2001); Beyond Lean manufacturing: Combining Lean and the Theory of Constraints for higher performance. Port Angeles, US.
Garza-Reyes, J.A.; Eldridge, S.; Barber, K. D.; Soriano-Meier, H. (2010); Overall equipment effectiveness (OEE) and process capability (PC) measures: a relationship analysis, International Journal of Quality & Reliability Management, 27, 48-62.
Goldratt, E M. ; Cox, J.F. (1984); A meta. 1. ed. São Paulo SP: Nobel.
Goldratt, E. M. (1996); A Síndrome do Palheiro - Garimpando Informações num Oceano de Dados. Editora Educator, São Paulo.
Goldratt, E. M. (2009); Standing on the shoulders of giants production concepts versus production applications: the Hitachi Tool Engineering example. Revista Gestão & Produção, v. 16, n. 3, p. 333-343.
Gupta, C. M.; Boyd, H.L. (2008); Theory of constraints: a theory for operations management, International Journal of Operations & Production Management, Vol. 28 Iss: 10 pp. 991 – 1012.
Hayes, R.; Pisano, G.; Upton, D.; Whellwright, S. (2008); Produção, estratégia e tecnologia: em busca da vantagem competitiva. Porto Alegre: Bookman.
Hopp, W. ; Spearman, M. L. (2001); Factory Physics. Boston: Irwin.
Jeong, K-Y.; Phillips, D. T. (2001); Operational efficiency and effectiveness measurement. International Journal of Operation & Production Management, 21, 1404–1416.
Ifandoudas, P.; Chapman, R. (2009); A practical approach to achieving Agility- a theory of constraints perspective,Production Planning and Control, 20, v.8, 691-702.
Inman, R. A.; Sale, M. L.; Green Jr., (2009); K. W. Analysis of the relationships among TOC use, TOC outcomes, and organizational performance, International Journal of Operations & Production Management, Vol. 29 Iss: 4, pp.341 – 356.
Mabin, V. J.; Balderstoone, S. J. (2003); The performance of the theory of constraints methodology: Analysis and discussion of successful TOC applications. International Journal of Operations & Production Management, v. 23, n. 6, p. 568-595.
Mathur, A; Dangayach, G.S.; Mittal, M.L.; Sharma, M. K. (2011); Performance measurement in automated manufacturing. Measuring Business Excellence, Vol. 15 Iss: 1 pp. 77 – 91.
Muthiah, K.M.N.; Huang, S.H. (2007); Overall throughput effectiveness (OTE) metric for factory-level performance monitoring and bottleneck detection, International Journal of Production Research, Vol. 45 No. 20, pp. 4753-69.
Muthiah, K.M.N., Huang, S.H.; Mahadevan, S. (2008); Automating factory performance diagnostics using overall throughput effectiveness (OTE) metric, International Journal of Advanced Manufacturing Technology, Vol. 36 Nos 7/8, pp. 811-24.
Nakalima, S. (1988); Introduction to TPM - Total Productive Maintenance. Cambridge, MA: Productivity Press,
Rahman, S. (1998); Theory of constraints: A review of the philosophy and its applications , International Journal of Operations & Production Management, Vol. 18 Iss: 4 pp. 336 – 355.
Ronen, B.; Pass, S. (2010); Services Management in The Theory of Constraints Handbook, 1st Edition, Cox III, J.F. & Schleier, J.G., (Eds), McGraw-Hill, New York.
Rose, E.; Odom, R.; Dumbar, R.; Hinchman, J. (1995); How TOC & TPM work together to build the quality toolbox of SDWTs, in Electronics Manufacturing Technology Symposium, Manufacturing Technologies - Present and Future, Seventeenth IEEE/CPMT International, Austin, TX , USA, 56-59.
Scott, D.; Pisa, R. (1998); Can overall factory effectiveness prolong Moore’s law? Solid StateTechnology, Vol. 41 No. 3, pp. 75-82.
Umble, M.M.; Srikanth, M.L. (1995); Synchronous Manufacturing: principles for world class excellence. Cincinnati, South-Western.
Umble, M. M; Umble, E. J. (1999); Drum-Buffer-Rope for Lower inventory. Industrial Management, p. 24-33, September-October.
Wakjira, M. W.; Singh, A. P. (2012); Total Productive Maintenance: A Case Study in Manufacturing Industry. Global Journal of Researches in Engineering Industrial Engineering, p. 24-32, Vol 12.
Walsh, D. P. (2010); Complex Environments in The Theory of Constraints Handbook, 1st Edition, Cox III, J.F. & Schleier, J.G., (Eds), McGraw-Hill, New York.
Watson, K.J. ; Patti, A. (2008); A comparison of JIT and TOC buffering philosophies on system performance with unplanned machine downtime, International Journal of Production Research, Vol. 46 No. 7, pp. 1869-85.