1. Introdução
Ao longo dos últimos anos, o setor elétrico brasileiro passou por mudanças estruturais em sua regulamentação, a exemplo do que ocorreu em diversos países de todo o mundo. Para que o sistema energético do estado do RS, Brasil, não entre em colapso, um dos estudos necessário é o da análise do número de consumidores e do consumo de energia gerada. Técnicas de modelagem matemática podem ser empregadas para auxiliar os gestores na verificação da tendência geral das séries, identificando os seus movimentos no curto, médio e longo prazo, possibilitando o conhecimento de suas características.
O crescimento econômico do estado do Rio Grande do Sul, assim como do restante do país, está intimamente ligado à distribuição e à geração de energia elétrica. Dessa forma, o objetivo desta pesquisa é analisar conjuntamente, por meio da análise de componentes principais, o comportamento do número de consumidores e do consumo em MWh de energia elétrica do Rio Grande do Sul, com o uso de modelos de previsão lineares e não lineares, das companhias CEEE, AES-Sul e RGE.
A pesquisa foi estruturada em cinco itens: o primeiro apresenta a introdução, o objetivo geral e os específicos. No item dois encontra-se a revisão de literatura. A metodologia apresenta-se no item três; no item quatro, as análises e discussões e, por fim, no item cinco, as considerações finais, seguida das referências.
2. Referencial teórico
Aborda-se, neste item, a análise de componentes principais (ACP), os modelos lineares da classe geral ARIMA e os modelos não lineares ARCH.
2.1 Análise de componentes principais
O método de Análise de Componentes Principais (ACP) foi desenvolvido por Pearson (1901) e, posteriormente, por Hotelling (1933). Essa técnica vem sendo estudada por autores como Seber (1984), Reinsel (1993), Jackson (1980, 1981) e Johnson e Wichern (1992, 1998). A ideia central é a redução do conjunto de dados a serem analisados, principalmente quando os dados são constituídos por um grande número de variáveis inter-relacionadas.
Para determinar as componentes principais (CP), é necessário encontrar a matriz de correlação ou a matriz de variância-covariância, de onde é possível encontrar os autovalores () e autovetores () que possibilitam escrever uma combinação linear, a qual é denominada de CP (REIS, 2001).
Para satisfazer as condições de normalidade e ortogonalidade às CP, utiliza-se o método do multiplicador de Lagrange na solução da equação 1 (Morrison, 1976).
(1) |
Da equação 1, encontram-se os autovalores e autovetores que possibilitam escrever cada componente principal, representada conforme (2).
(2) |
Em (2), cada corresponde ao vetor de constantes que deve manter a condição de normalidade, isto é, ![]() para que o sistema tenha solução única e de ortogonalidade, isto é,
para que o sistema tenha solução única e de ortogonalidade, isto é, ![]() para i ≠ k com i,k = 1,..., p, que garante que as componentes principais sejam independentes.
para i ≠ k com i,k = 1,..., p, que garante que as componentes principais sejam independentes.
A explicação de cada componente principal é medida em termos de variância (Corrar, Dias Filho, 2007). Logo, tem-se que o quociente é expresso em percentagem:
 , |
(3) |
Sendo que essa expressão representa a proporção da variância total explicada.
Alexander (2005) salienta que a análise de componentes principais é um dos métodos mais simples e importantes na extração de informações de dados de fontes autocorrelacionadas em um sistema multivariado e que também são úteis para revelar as volatilidades implícitas das diversas opções de um mesmo ativo financeiro. Do descrito acima, a técnica torna-se útil para se reduzir a dimensão do problema a ser estudado e poder ser analisada por métodos de modelagem como os propostos neste estudo.
2.2 Modelos lineares e não lineares de previsão
Os modelos lineares - autorregressivos integrados e de médias móveis (ARIMA) - são úteis para tratar a autocorrelação presente em séries de dados obtidos sequencialmente no tempo, modelando a média condicional de uma série, quando a variância dos erros é assumida constante. E os modelos não lineares, autorregressivos condicionais a heterocedasticidade (ARCH) possuem a propriedade de modelar a variância condicional, quando os resíduos não apresentarem-se homocedásticos.
De acordo com Box e Jenkins (1970) e Moretin (2006), um processo segue um processo ARIMA (p,d,q) se:
(4) |
onde é operador retroativo ou operador de defasagens, é inteiro positivo e representa a diferença, conforme a ordem de integração; e são os parâmetros dos processos autorregressivos e de média móvel de ordem e , respectivamente, e é ruído branco.
A construção de modelos ARIMA segue um ciclo iterativo da metodologia de Box e Jenkins, que é composto por quatro etapas: a) identificação; b) estimação; c) verificação do diagnóstico e d) previsão (Gujarati, 2000). Esses modelos também são discutidos pelos autores Box, Jenkins e Reinsel (1994), Makridakis, Wheelwright e Hyndman (1998), Morettin e Toloi (2004). A ferramenta principal para a identificação das séries temporais são as funções de autocorrelação (FAC) e a autocorrelação parcial (FACP), que auxiliam na determinação do tipo e a ordem do modelo (MORETTIN, 2008).
No caso de uma série temporal apresentar uma periodicidade que ocorre dentro do período de um ano, ela é denominada sazonal e é representada por um período de repetição S, em que S = 3, 4, 6, ..., S representam sazonalidades de ordem trimestral, quadrimestral e, assim, sucessivamente. A periodicidade pode ser incorporada ao modelo por meio da utilização de um modelo ARIMA sazonal, denominado SARIMA (p,d,q) (P,D,Q)s, como representado na equação 5.
(5) |
Em que S é o período da sazonalidade, e são os parâmetros dos processos autorregressivos e de média móvel de ordem e , respectivamente, representando a parte não sazonal. Os parâmetros e correspondem à parte autorregressiva e de médias móveis da parte sazonal representadas por P e Q. A parte integrada é representada por a diferenciação simples de ordem d, é a diferenciação sazonal de ordem D e é o ruído branco.
A modelagem linear representada pelos modelos ARIMA será útil para estimar os modelos que representarão CP se estas forem autocorrelacionadas. Os resíduos oriundos da modelagem ARIMA serão investigados em relação à sua homocedasticidade. Se essa característica estiver presente, utilizam-se os modelos não lineares ARCH.
Os Modelos Autorregressivos de Heterocedasticidade Condicional (ARCH) tiveram o seu surgimento com o pesquisador americano Robert Engle (1982), que observou que os dois primeiros momentos de uma série temporal (média e variância) não são captados conjuntamente pelos modelos lineares. Geralmente, os modelos ARIMA, embora produzindo resíduos do tipo ruído branco, quando analisados na sua forma quadrática, não apresentam um comportamento aleatório puro.
Os modelos propostos por Engle dão um passo a mais e verificam a existência de heterocedasticidade nos resíduos, a qual é denominada volatilidade (BUENO, 2008). A idéia básica desses modelos é a de que os resíduos da série não sejam correlacionados serialmente, mas dependentes, e essa dependência pode ser descrita por uma função quadrática de seus valores passados. Dessa forma, a série de resíduos pode possuir média zero e não ser autocorrelacionada, mas a série dos seus valores quadráticos pode apresentar autocorrelação serial e, por isso, são denominados de modelos não lineares.
A idéia principal do modelo ARCH é o fato de que a variância de , no período de tempo , depende de . O termo de erro , condicionado à informação disponível no período (t-1).
Um modelo ARCH(m), em que denota a ordem do modelo, expressa a variância condicional do modelo anterior para a média condicional como uma função das inovações quadráticas passadas (Silva, Sáfadi, Castro Júnior, 2005). Segundo Morettin (2008), o modelo ARCH(m) é definido por:
|
(6) |
Pode-se observar que a variância condicional ao erro et, para a informação disponível no tempo (t-1), pode ser distribuída, conduzindo a expressão 7.
(7) |
Nesse caso, o modelo ARCH (1), que representa a variância condicional, pode ser representado por 8.
(8) |
|
|
(9) |
||
onde et é independente e identicamente distribuído (i.i.d) com média zero e a variância condicional. Para assegurar que a variância condicional seja positiva e fracamente estacionária, as seguintes restrições paramétricas são necessárias: A0 > 0, A0 > 0 para todo e![]() .
.
Os parâmetros do modelo ARCH, indicam a velocidade com que a variabilidade se propagará no tempo, então, de posse de um valor previsto ou do comportamento de uma série, é possível antever o seu impacto no tempo futuro. Maiores detalhes sobre os modelos ARCH encontram-se em Campos (2007), Morettin (2006), Bueno (2008), Enders (1995) e Hamilton (1994).
3. Metodologia
A análise refere-se ao número de consumidores e ao consumo de energia elétrica medidas em unidades megawatts hora (MWh) no estado do RS, coletados mensalmente no período de janeiro de 1998 a dezembro de 2009 das três maiores distribuidoras de energia elétrica, nomeadamente a AES-Sul, CEEE e RGE. Não são consideradas, neste estudo, as cooperativas de energia elétrica ou de geração própria de energia, que são responsáveis por menos de 6% de geração e distribuição.
Os setores analisados dessas distribuidoras são: industrial, comercial, rural, serviços públicos, residencial e outros apresentados na Tabela 1. A coleta de dados foi realizada na Fundação de Economia e Estatística do Rio Grande do Sul, que reúne informações de natureza socioeconômica relativas ao estado e a seus municípios.
Tabela 1 – Distribuidoras de energia elétrica e regiões de abrangência no RS
| Companhias Estaduais de Distribuição de Energia Elétrica para o Rio Grande do Sul | ||
Distribuidoras |
Setores |
Área de Concessão |
CEEE |
Residencial Comercial Industrial Rural Serviços Públicos Outros |
Regiões metropolitanas de Porto Alegre, litoral e campanha gaúcha. |
AES-Sul |
Regiões metropolitanas e centro-oeste do estado. |
|
RGE |
Região norte-nordeste do estado do Rio Grande do Sul. |
|
As etapas metodológicas a serem seguidas são as seguintes:
Etapa 1: Análise de Componentes Principais – (ACP): extração e seleção das CP utilizando a matriz de correlação, como forma de padronizar as variáveis sob análise, representativas de cada distribuidora nos diversos setores e diversas companhias. O objetivo é analisar o comportamento conjunto dos setores de distribuição de cada distribuidora.
Etapa 2: Modelagem linear – ARIMA (p, d, q): utilizam-se as CP selecionadas na etapa 1 para estimar o provável modelo da classe geral ARIMA, de modo que represente um ruído branco. O melhor modelo selecionado terá os seus resíduos investigados em relação à homocedasticidade, por meio do teste LM-ARCH (SILVA, SÁFADI e CASTRO JÚNIOR, 2005).
Etapa 3: Modelagem não linear – ARCH (m): O objetivo da modelagem ARCH é considerar os efeitos da volatilidade conjuntamente com os da média do processo. Nessa etapa, os passos metodológicos são semelhantes ao passo 2, apenas com o diferencial de que a variável em estudo passa a ser a série de resíduos quadráticos do melhor modelo ARIMA selecionado. Depois de estimado o modelo conjunto ARIMA-ARCH, realiza-se a análise dos resíduos novamente em busca de resíduos ruído branco.
4. Apresentação e análise dos resultados
O aumento do PIB no estado do Rio Grande do Sul tem sido acompanhado pelo aumento dos níveis de consumo de energia elétrica nos últimos anos. Quanto ao perfil do consumo de energia elétrica, é o setor industrial que mais consome energia, com 37,72%. O setor residencial é responsável por 25,68%, o comercial por 16,84% e as áreas rurais por 12,54%. Com relação às cooperativas de eletrificação rural, apesar de 67% dos consumidores serem rurais, consomem somente 52,32% da energia elétrica distribuída, enquanto o setor industrial, com 0,64% dos consumidores, consome 23,23% da energia elétrica distribuída.
De acordo com entrevista do diretor-geral do Operador Nacional do Sistema Elétrico - ONS, Hermes Chipp (http://www.asef.com.br/Noticias%2002%2003%202010.htm) em vez de um único horário de pico, o sistema elétrico brasileiro apresentou, no verão de 2009, um segundo pico de energia. Bernini, no entanto, demonstra preocupação com o impacto do aumento de consumo residencial sobre a qualidade da distribuição da energia nas grandes cidades.
4.1 Análise de componentes principais
A determinação da combinação linear por meio da ACP possibilita que se encontre um conjunto de dados não correlacionados contendo informações de todos os setores de energia elétrica de cada concessionária. A técnica também permite por inspeção de suas cargas fatoriais quais setores possuem maior influência na formação da CP, possibilitando assim uma ordenação do grau de importância dos setores na composição de cada CP.
4.1.1 Análise do número de consumidores e consumo de energia elétrica por classe de consumo no Rio Grande do Sul para CEEE, AES-Sul e RGE
Na Tabela 2, são apresentados os números de CP selecionadas, os autovalores e o percentual de variância explicada, oriundos da matriz de correlação.
Tabela 2 – Autovalores e variância explicada de cada componente para o número de consumidores e consumo de energia elétrica no RS
| Autovalores extraídos para o número de consumidores de energia elétrica | |||
| Concessionária | Número de CP | Autovalores | % da Var. explicada |
| CEEE | 1 |
5,36 | 89,41 |
1 |
4,57 | 76,20 | |
| AES-Sul | 1 |
3,94 | 65,65 |
| RGE | 2 |
1,34 | 22,33 |
| Autovalores extração das CP para o consumo de energia elétrica | |||
| CEEE | 1 | 3,74 |
62,30 |
| 2 | 1,12 |
18,60 | |
| AES-Sul | 1 | 4,49 |
74,83 |
| RGE | 1 | 3,75 |
62,50 |
| 2 | 1,04 |
17,28 | |
Nota: Para a extração dos autovalores, utilizou-se a matriz de correlação, e foram selecionados aqueles autovalores superiores a 1 (KAISER, 1960).
- Número de consumidores
Analisando o número de consumidores da CEEE, a CP1CEEE representa 89,41% de variância explicada dos setores de distribuição. Logo, em vez de utilizar os seis setores que representam as classes de número de consumidores, passa a ser utilizada apenas uma CP1CEEE, com uma perda de informação de aproximadamente 10,59% das variáveis originais.
Para a AES-Sul, constata-se que a CP1AES-Sul representa 76,20% de variância explicada, com uma perda de informação de aproximadamente 23,8% das variáveis originais.
Para a distribuidora RGE, foram selecionadas as CP1RGE, que representa 65,65%, e a CP2RGE, que representa 22,33% da variabilidade das variáveis pesquisadas, representando uma variância explicada acumulada de 87,98%, com uma perda de informação de aproximadamente 12,02% das variáveis originais.
A partir desta análise, em vez de utilizar as seis variáveis que compõem os setores do número de consumidores, passam a serem utilizadas apenas as CP selecionadas, que serão utilizadas nas etapas de modelagem futura pelo fato de não apresentarem correlacionadas, mas ainda assim mantém a autocorrelação presente nos dados.
- Consumo de Energia
Para a distribuidora CEEE, duas CP, que representam 80,9% das variáveis originais. Constata-se que CP1CEEE representa 62,30% das variáveis pesquisadas, e a CP2CEEE representa 18,60% das variáveis originais.
Para a distribuidora AES-Sul, a CP1AES-Sul representa 74,83% da variabilidade das variáveis pesquisadas. A partir dessa análise, em vez de utilizar as seis variáveis, passa a ser utilizada apenas uma CP, representada pelos seus autovalores superiores a 1, com uma perda de informação de aproximadamente 25,17% das variáveis originais.
Para a distribuidora RGE, consideram-se as CP1RGE, que representa 65,50%, e a CP2RGE, que representa 17,28% da variabilidade das variáveis pesquisadas, com variância explicada acumulada de 79,78%.
Vale lembrar que outro critério de seleção do número de CP foi atendido, aquele que encerra um grau de explicação de no mínimo 70% da variabilidade total do conjunto de dados original (Marchezan, Souza, Menezes, 2011).
Na Tabela 3, são mostradas as cargas fatoriais de cada variável na composição da componente principal selecionada.
Tabela 3 – Cargas fatoriais por companhia do número de consumidores e do consumo de energia elétrica
|
CP do número de consumidores |
CP do consumo |
|||||||
CEEE |
AES-Sul |
RGE |
CEEE |
AES-Sul |
RGE |
||||
CP 1 |
CP1 |
CP 1 |
CP 2 |
CP 1 |
CP2 |
CP1 |
CP 1 |
CP 2 |
|
Res |
-0,94 |
-0,44 |
-0,97 |
-0,21 |
-0,86 |
0,08 |
-0,94 |
0,24 |
0,26 |
Com |
-0,98 |
-0,46 |
-0,98 |
-0,15 |
-0,92 |
0,31 |
-0,98 |
0,26 |
0,09 |
Ind |
0,76 |
0,36 |
-0,32 |
0,76 |
0,44 |
0,82 |
0,74 |
0,14 |
-0,78 |
Rural |
-0,79 |
-0,37 |
-0,96 |
-0,08 |
-0,84 |
-0,20 |
-0,77 |
0,23 |
0,27 |
S Publ |
-0,84 |
-0,39 |
-0,98 |
-0,01 |
-0,84 |
0,47 |
-0,82 |
0,24 |
-0,32 |
Outros |
-0,91 |
-0,43 |
0,23 |
-0,83 |
-0,73 |
-0,29 |
-0,94 |
0,12 |
0,32 |
A variável com maior correlação com a CP1CEEE é a variável nominada “Com” – setor comercial (0,98), seguida das variáveis “Res” e representa o setor residencial (-0,94), Outros – setor outros (0,91), “S Publ” – setor serviços públicos (-0,84), Rural – setor rural (-0,79). Verificando na Tabela 1, observa-se que a CEEE atende as áreas de concessão da região metropolitana de Porto Alegre, litoral e campanha.
A análise para as demais distribuidoras devem ser realizadas de maneira análoga, onde é possível ordenar da maior para a menor carga fatorial o grau de contribuição de cada setor na CP. O mesmo procedimento deve ser mantido para o consumo de energia. Vale lembrar que apenas as CP selecionadas estão representadas na Tabela 3.
A ACP é um recurso muito útil, porque permite uma grande redução das dimensões e a ordenação natural do sistema e ainda fornece uma interpretação significativa das componentes principais (Alexander, 2005). Além disso, essa análise facilita, em grande parte, a avaliação do movimento da volatilidade, vinculada a oscilações de demanda e ao fornecimento de energia elétrica.
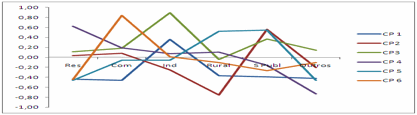
Considerando o número de consumidores, o deslocamento da primeira CP representa os movimentos paralelos de ascendência e descendência, portanto, uma mudança que ocorra em uma das variáveis que compõe a componente principal se refletirá nesta componente. Por essa razão, a primeira componente principal é chamada componente de tendência das curvas, neste caso, 89,41% da variação total da distribuidora CEEE (a), 76,20% da variação total da distribuidora AES-Sul (b) e 87,98% da variação total da distribuidora RGE (c), conforme Figuras 1a, 1b e 1c.

(a)
(b)

(c)
Figura 1 – Gráfico das CP para as distribuidoras CEEE (a), AES-Sul (b) e RGE (c)
para o número de consumidores de energia elétrica para o Rio Grande do Sul.
Pode-se perceber, analisando a Figura 1, que a ACP, além de reduzir as dimensões a serem analisadas, as componentes selecionadas são capazes de acompanhar os movimentos das mudanças de todas as curvas em análise, devido à elevada correlação que é refletida pelas cargas fatoriais da primeira componente para CEEE e AES-Sul e para a primeira e a segunda componentes para a RGE, são muito próximas a 1.
Os resultados da ACP para o consumo de energia, cujas cargas fatoriais são mostradas na Tabela 3, em que se observa que as correlações são bastante elevadas, e isso se reflete nas semelhanças das cargas fatoriais da primeira e segunda componente principal para as distribuidoras CEEE e RGE. Já, a AES-Sul é representada por uma componente principal. A primeira componente principal é chamada componente de tendência das curvas, neste caso, 80,9% da variação total da distribuidora CEEE (a), 74,83% da variação total da distribuidora AES-Sul (b) e 79,78% da variação total da distribuidora RGE (c). O deslocamento da componente principal provoca uma inclinação da curva das cargas fatoriais do número de consumidores de energia elétrica, conforme Figura 2a, 2b e 2c.

(a)

(b)

(c)
Figura 2 – Gráfico das cargas fatoriais para as distribuidoras CEEE (a), AES-Sul (b) e RGE (c) para o número de consumidores de energia elétrica para o Rio Grande do Sul.
Pode-se perceber, analisando a Figura 2, que a ACP foi capaz de reduzir as dimensões e que as componentes selecionadas acompanham o movimento das mudanças de todas as curvas em análise para a CEEE e para a AES-Sul, sendo a primeira e a segunda componente para a RGE muito similares. Essas CP serão analisadas segundo os modelos ARIMA e/ou ARCH.
4.2 Modelos de lineares e não lineares para as CP selecionadas
No setor elétrico, a projeção constitui a base no processo de planejamento de investimentos em termos técnicos e estratégicos, sendo que a energia necessária a ser contratada pelas empresas distribuidoras advém do estudo das projeções de demanda.
Um estudo de verificação da presença de autocorrelação e da estacionariedade das CP´s foi realizada por meio da construção de correlogramas, os quais mostraram que todas as CP selecionadas para o estudo mostram-se não estacionárias com características sazonais. Além da FAC e FACP, utilizaram-se os testes de raiz unitária Augmented Dicky Fuller ADF (1979) e Kwiatkowski-Phillips-Schmidt-Shin – KPSS (1992), que possibilitaram determinar se as séries eram não estacionárias. Os resultados estão refletidos nos modelos não estacionário da Tabelas 5 e 6, onde as séries não estacionárias foram representadas por um modelo ARIMA e as estacionárias por um modelo ARMA.
- Modelo para as CP representativas do número de consumidores de energia elétrica do RS
O número de consumidores é o foco principal das empresas, pois a competição pela conquista de mercado faz com que estas planejem o futuro de uma maneira mais complexa, envolvendo aspectos estratégicos, incertezas e, muitas vezes, limitações de informações. Na Tabela 5, apresentam-se os modelos para as CP selecionadas das companhias CEEE, AES-Sul e RGE, levando em consideração os seis setores, que são: residencial, comercial, industrial, rural, serviços públicos e a classificação outros.
Tabela 5 – Modelos lineares e não lineares aplicados às CP e suas estatísticas de modelagem para o número de consumidores de energia elétrica no RS
| CP1CEEE - ARIMA(1,1,0) – ARCH(1) | |||||||||||||||||||||||||||
Equação representativa da média - ARIMA(1,1,0) |
|||||||||||||||||||||||||||
d=1 |
Coeficiente |
D.Padrão |
t-statistic |
Prob. |
AIC |
DW |
JB |
||||||||||||||||||||
|
0.254690 |
0.081136 |
3.139057 |
0.002 |
-3.114 |
2.068 |
7.559 |
||||||||||||||||||||
LM- ARCH test: TR² = 18,35 com |
|||||||||||||||||||||||||||
Método: ML – ARCH (Marquardt) – Distribuição Normal |
|||||||||||||||||||||||||||
Equação para variância condicional |
|||||||||||||||||||||||||||
|
Coeficiente |
Erro-Padrão |
Estatística Z |
p-valor. |
|||||||||||||||||||||||
α |
0,83 |
0,09 |
-3,79 |
0,002 |
|||||||||||||||||||||||
|
0,47 |
0,14 |
3,50 |
0,005 |
|||||||||||||||||||||||
LM- ARCH test: TR² = 0,02 com |
|||||||||||||||||||||||||||
CP1AES-Sul - ARIMA(1,1,1) |
|||||||||||||||||||||||||||
d=1 |
Coeficiente |
D.Padrão |
t-statistic |
Prob. |
AIC |
DW |
JB |
||||||||||||||||||||
|
-0.424419 |
0.078284 |
-5.421546 |
0.0000 |
-0.4389 |
1.861 |
5.106 |
||||||||||||||||||||
|
-0.859849 |
0.046902 |
-18.33277 |
0.0000 |
|||||||||||||||||||||||
LM- ARCH test: TR² = 1,59 com |
|||||||||||||||||||||||||||
CP1RGE - SARIMA(1,1,0)(1,0,0)12 |
|||||||||||||||||||||||||||
d=1 |
Coeficiente |
D.Padrão |
t-statistic |
Prob. |
AIC |
DW |
JB |
||||||||||||||||||||
|
0,24 |
0,006 |
2,750 |
0,006 |
-2,98 |
1,99 |
9,48 |
||||||||||||||||||||
|
0,19 |
0,091 |
2,075 |
0,039 |
|||||||||||||||||||||||
LM- ARCH test: TR² = 2,84 com |
|||||||||||||||||||||||||||
CP2RGE - ARIMA(1,1,0) |
|||||||||||||||||||||||||||
d=1 |
Coeficiente |
D.Padrão |
t-statistic |
Prob. |
AIC |
DW |
JB |
||||||||||||||||||||
|
0,35 |
0,078 |
4,476 |
0,000 |
-2,92 |
1,424 |
3447,162 |
||||||||||||||||||||
LM- ARCH test: TR² = 3,17 com |
|||||||||||||||||||||||||||
*AIC – Critério de Informação Akaike ; DW – Teste Durbin-Watson; JB – Teste Jarque-Bera
A modelagem ARCH é importante quando existe a presença de heterocedasticidade condicional, pois o Método de Mínimos Quadrados Ordinários não produz estimativas eficientes para seus parâmetros nem mesmo uma variância mínima (SILVA, 2000). Logo, a estimação conjunta produz melhores efeitos de estimativas.
Todos os modelos encontrados apresentaram resíduos com características de ruído branco. Para cada modelo estimado, seus resíduos foram tomados na sua forma quadrática e aplicados a eles o teste de hipótese ARCH-LM com o intuito de verificar a presença de heterocedasticidade condicional. Considerando-se as hipóteses ![]() não existem efeitos ARCH (homocedasticidade) vs.
não existem efeitos ARCH (homocedasticidade) vs. ![]() existem efeitos ARCH (heterocedasticidade), em que os resultados estão dispostos na Tabela 5, logo após cada modelo.
existem efeitos ARCH (heterocedasticidade), em que os resultados estão dispostos na Tabela 5, logo após cada modelo.
O modelo ARIMA (1,1,0) para a CP1CEEE mostrou evidências de características de volatilidade condicional, portanto, sugeriu-se uma estimação ARCH (1). O modelo apresentou parâmetros estatisticamente significativos, com parâmetro representativo da volatilidade igual a 0,47, o que significa que, após um curto período de tempo, a variância da série deverá convergir para a sua média histórica. Isto é, os setores que compõe a CP1CEEE no período anterior irão influenciar no próximo período, mas não de uma forma acentuada, mas que deve servir de alerta para os gestores dado que esta componente representa principalmente os setores comercial e residencial da região metropolitana de Porto Alegre, litoral e região da campanha, talvez devendo ser este o motivo de variabilidade no número de consumidores desta concessionária.
As demais CP, quando modeladas, não apresentaram comportamento volátil, o que pode ser explicado por dois fatores. O primeiro é que a CEEE encerra o maior grau de explicação das demais concessionárias, com um autovalor 5,36, portanto sendo encarregada de revelar a maior variabilidade existente. E outro fator pode ser devido à região de concessão. Dessa forma, pode-se dizer que, no período analisado, não há uma grande flutuação na série que venha a comprometer o comportamento global das estimativas da média do processo.
A modelagem de componentes principais por meio dos modelos ARIMA e/ou ARCH possibilita que, além da redução da dimensionalidade, ocorra a identificação dos principais setores formadores daquela componente. De acordo com Alexander (2005), a ACP é capaz de acompanhar o movimento conjunto de diversas curvas, o que possibilita uma eficácia no acompanhamento de todas as variáveis envolvidas no sistema. Além disso, a análise possibilita uma ordenação natural das variáveis envolvidas no processo.
- Modelo para as CP representativas do consumo de energia elétrica em KWh do RS
A demanda de potência é medida e expressa em KW, que corresponde à potência elétrica solicitada pelo consumidor à empresa distribuidora durante o período de fornecimento mensal. O consumo efetivo é medido e expresso em KWh, o qual corresponde ao real consumo ao longo do período faturado, normalmente de 30 dias. E, cujos modelos representativos estão na Tabela 6.
CP1CEEE - SARIMA(1,1,1)(1,0,0)12 |
||||||||||||||||
d=1 |
Coeficiente |
D.Padrão |
t-statistic |
Prob. |
AIC |
DW |
JB |
|||||||||
|
0,36 |
0,113 |
3,163 |
0,002 |
1,934 |
1,944 |
7,469 |
|||||||||
|
-0,62 |
0,070 |
-8,895 |
0,000 |
||||||||||||
|
-0,88 |
0,054 |
-16,281 |
0,000 |
||||||||||||
LM- ARCH test: TR² = 0,55 com |
||||||||||||||||
CP2CEEE - ARIMA(1,1,1) |
||||||||||||||||
d=1 |
Coeficiente |
D.Padrão |
t-statistic |
Prob. |
AIC |
DW |
JB |
|||||||||
|
0,57 |
0,095 |
5,950 |
0,000 |
1,879 |
1,961 |
6,060 |
|||||||||
|
-0,89 |
0,050 |
-17,813 |
0,000 |
||||||||||||
LM- ARCH test: TR² = 0,129 com |
||||||||||||||||
CP1AES-Sul - SARIMA(0,1,1)(1,0,0)12 |
||||||||||||||||
d=1 |
Coeficiente |
D.Padrão |
t-statistic |
Prob. |
AIC |
DW |
JB |
|||||||||
|
-0,410 |
0,077 |
-5,313 |
0,000 |
1,165 |
1,811 |
7,469 |
|||||||||
|
-0,857 |
0,041 |
-20,860 |
0,000 |
||||||||||||
LM- ARCH test: TR² = 2,432 com |
||||||||||||||||
CP1RGE - SARIMA(0,1,2)(1,0,1)6 |
||||||||||||||||
d=1 |
Coeficiente |
D.Padrão |
t-statistic |
Prob. |
AIC |
DW |
JB |
|||||||||
|
-0,941 |
0,043 |
-21,656 |
0,000 |
2,456 |
1,619 |
0,438 |
|||||||||
|
-1,929 |
0,018 |
-106,573 |
0,000 |
||||||||||||
|
0,930 |
0,017 |
53,146 |
0,000 |
||||||||||||
|
0,431 |
0,098 |
4,387 |
0,000 |
||||||||||||
LM- ARCH test: TR² = 4,060 com |
||||||||||||||||
CP1RGE - SARIMA(0,1,1)(1,0,1)6 |
||||||||||||||||
d=1 |
Coeficiente |
D.Padrão |
t-statistic |
Prob. |
AIC |
DW |
JB |
|||||||||
|
-0,553 |
0,079 |
-6,947 |
0,000 |
1,923 |
2,092 |
294,90 |
|||||||||
|
-0,688 |
0,064 |
-10,746 |
0,000 |
||||||||||||
|
-0,783 |
0,060 |
-13,007 |
0,000 |
||||||||||||
LM- ARCH test: TR² = 0,490 com |
||||||||||||||||
*AIC – Critério de Informação Akaike ; DW – Teste Durbin-Watson; JB – Teste Jarque-Bera
Observa-se que todos os parâmetros são significativos, tanto dos modelos que representam o número de consumidores, quanto os que representam o consumo. Os modelos encontrados apresentam características de ruído branco e estatísticas de validação do modelo adequadas.
Observa-se que, nos gráficos dos valores previstos, a série estimada dentro da amostra mantém comportamento similar com a da componente principal, sendo, assim, possível determinar as possíveis mudanças de inclinação, bem como deslocamentos de magnitudes que podem servir de auxílio aos tomadores de decisão.
5. Considerações finais
A metodologia proposta foi capaz de acompanhar e determinar o movimento das séries em estudo de forma global, fornecendo subsídios para os tomadores de decisão, revelando as tendências e as oscilações das CP, de modo que não seja necessário se fazer uma análise individual de cada setor de cada distribuidora.
Conclui-se que o procedimento proposto, de primeiro aplicar a ACP aos dados para depois ajustá-los a um modelo matemático, mostrou-se importante, pois foi possível eliminar a correlação entre as variáveis e tratar a multicolinearidade. Ao estudar a autocorrelação dos dados utilizando os modelos ARIMA e os modelos ARCH, obteve-se uma nova perspectiva de aprendizagem sobre o processo através das informações contidas na estrutura da CP. Além disso, a investigação da estabilidade do processo se faz por meio da verificação da influência da volatilidade na detecção de clusters de volatilidade, que são potenciais para afetar o desempenho do processo produtivo.
Dessa forma, sustenta-se que os modelos de previsão lineares e não lineares podem ser aplicados conjuntamente para melhor captarem os movimentos globais das companhias em estudo e do número de consumidores visando, com isso, a um crescimento de informações para a correta tomada de decisão.
Esta pesquisa ficou delimitada geograficamente pelas companhias e usuários do Rio Grande do Sul, pela utilização de técnicas de modelos lineares da classe geral ARIMA e pelos modelos não lineares ARCH. Além dessas delimitações citadas, deve-se ressaltar que os modelos de previsões aqui utilizados serão capazes de fornecer o movimento geral da curva, sem que seja possível especificar valores previstos individualmente, pois se procurou estudar os movimentos ascendentes e descendentes.
Deixa-se como sugestão de estudo a realização das previsões individuais das variáveis em estudo com o intuito de se obter valores individuais de previsões por setores, assim como a utilização de outros modelos de volatilidade como o Generalized Autoregressive Conditional Heteroskedsticity (GARCH) e Integrated Generalized Autoregressive Conditional Heteroskedsticity (IGARCH), para verificar se as séries que não apresentaram volatilidade utilizando os modelos ARCH não apresentam essas outras características.
Agradecimentos
Os autores agradecem a Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - CAPES - BEX 1784/09-9. Os autores também agradecem ao suporte financeiro providenciado pela Fundação para a Ciência e Tecnologia (FCT) sob grants número PTDC/GES/73418/2006 e número PTDC/GES/70529/2006. Também agradecemos aos revisores anônimos pelas suas sugestões para melhorar o texto.
Referências
Alexander, C. (2005); “Modelos de Mercado: um guia para a Análise de Informações Financeiras/Carol Alexander” Trad: José Carlos de Souza e Santos. São Paulo: Bolsa de Mercadorias & Futuros.
Baillie, R.; Chung, C. F.; Tieslau, M. A. (1996); “Analyzing inflation by the fractionally integrated ARFIMA-GARCH model”, Journal of Applied Econometrics. 11: 23-40.
Bartlett, M. S. (1946); “On the theoretical specification and sampling properties of autocorrelated time-series”, Journal of the Royal Statistical Society Supplement. 8: 27–41.
Bayer, F. M.; Souza, A. M.(2007); “Modelagem e previsão da taxa de ocupação hospitalar por meio de equações simultâneas: uma ferramenta de gestão.” GEPROS – Gestão de Produção, Operações e Sistemas. Ano 2, v. 2. mai./jun. p. 85-96.
Bem, A. B.(1998); A utilização de regressão dinâmica para prever a demanda por matrícula no ensino fundamental em Santa Catarina. 183f. (Dissertação em Engenharia de Produção) – Universidade Federal de Santa Catarina. Florianópolis.
Bollerslev, T (1986); “Generalized autoregressive conditional heteroskedasticity”, Journal of Econometrics. v. 31. p. 307-327.
Box, G. E. P.; Jenkins, G. M. (1970); Time Series Analysis:Forecasting and Control. San Francisco: Holden-Day.
Box, G. E. P.; Jenkins, G. M.; Reinsel, G. C. (1994); Time series analysis: forecasting and control. 3. ed. San Francisco: Holden-Day.
Bueno, Rodrigo de Losso da Silveira (2008); Econometria das séries temporais. São Paulo: Cengage Learning.
Campos, K. C. (2007); “Análise da volatilidade de preços de produtos agropecuários no Brasil”, Revista de Economia de Agronegócio. v. 5, n. 3. p. 303-328.
Corrar, J. L.; Paulo, E.; Dias Filho, J. M. (2007); “Análise multivariada para os cursos de administração, ciências contábeis e economia”, FIPECAF – Fundação Instituto de Pesquisas Contábeis, Atuariais e Financeiras. São Paulo: Atlas.
Dyner, I.; Larsen, E. R. (2001); “From Planning to Strategy in the Electricity Industry”, Energy Policy. n. 29. p. 1145-1154.
Élin Duxus Consultorie e Ltda. In: Manual e ajuda para o add-in Metrixus: Funções quantitativas para o mercado de capitais. [Acesso em: 18 jun. 2009]. Disponível em: http://www.duxus.com.br/produtos/tecnologia/addin/metrixus/manual/ajuda.php.
Enders, W. (1995); “Applied econometric time series”, Wiley series in probability and mathematical statistics. New York, NY: John Wiley and Sons, Inc.
Engle, R. F.(1982); “Autoregressive conditional heteroscedasticity with estimates of the variance of U.K. inflation”, Econometrica. 50: 987-1008.
FEE – Fundação de Economia e Estatística. [Acesso em: 10 mar. 2010]. Disponível em: http://www.fee.rs.gov.br.
Gujarati, D. N. (2000); Econometria básica. São Paulo: Makron Books..
Hamilton, J. (1994); Time series analysis. New Jersey: Princetor University Press.
Hottelling, H. (1933); “Analysis of a complex of Statistical variables into principal components”, The Journal of Educational Psychology. v. 24. p. 417-441/498-520.
Issler, J. V. (1999); “Estimating and Forecasting the Volatility of Brazilian Finance Series Using ARCH Models”, The Brazilian Review of Econometrics. v. 19, n. 1, p. 5-56.
Jackson, G.; Jones, G. K.(1999); “Spatial and temporal variation in nearshore fish and macroinvertebrate assemblage from a temperate Australian estuary over a decade”, Marine Ecology-Progress Series. Oldendorf, 182: 253-268.
Johnson, R. A.; Wichern, D. W. (1992); Applied multivariate statistical analysis. 3. ed. New Jersey: Prentice-Hall.
Li, Q.; Tricaud, C.; Sun, R.; Chen, Y. Q. (2007); Great salt lake surface level forecasting using figarch modeling. Proceedings of International Design Engineering Technical Conferences & Computers and Information in Engineering Conference IDETC/CIE (DETC2007-34909), Las Vegas, Nevada, USA, set. p. 4-7.
Maddala, G. S.(1992); Introduction to econometrics. 2. ed. New Jersey: Prentice-Hall Inc. Englewood Cliffs.
Makridakis, S. G.; Wheelwright, S. C.; Hyndman, R. J.(1998); Forecasting: methods and applications. 3. ed. New York: John Willey & Sons, Inc.
Morettin, P. A. (2006); Econometria financeira:um curso em séries temporais financeiras. 17º Simpósio Nacional de Probabilidade e Estatística. ABE. Caxambu.
Morettin, P. A.; Toloi, C. M. C.(2004); Análise de Séries Temporais. São Paulo: Edgard Blücher.
Morrison, D. F. (1976); Multivariate Statistical Methods.New York: McGraw-Hill.
Pearson, K. Phil. Mag. J.v. 6. 1901. p.559. PORTAL SÃO FRANCISCO. [Acesso em: 10 mar. 2010]. Disponível em: http://www.portalsaofrancisco.com.br/alfa/historia-da-eletricidade-no-brasil/historia-da-eletricidade-no-brasil-1.php.
Quenouille, M. H. (1949); “Approximate Tests of Correlation in Time-Series”, Journal of the Royal Statistical Society. 11: 68-84, 1949.
Reinsel, G. C. (1993); Elements of multivariate time series analysis. New York: Springer-Verlag.
Reis, E.(2001); Estatística multivariada aplicada. 2. ed. Ed. Sílabo.
Sáfadi, T.; Andrade Filho, M. G. (2007): “Abordagem Bayseana de modelos de séries temporais”, 12ª Escola de Séries Temporais e Econometria. ABE/SBE. 2007.
SCP-RS. [Acesso em: 10 mar. 2010]. Disponível em: http://www.scp.rs.gov.br/atlas/atlas.asp?menu=647.
Silva, W. S.; Sáfadi, T.; Castro Júnior, L. G. de. (2005); “Uma análise empírica da volatilidade do retorno de commodities agrícolas utilizando modelos ARCH: os casos do café e da soja”, Revista de Economia e Sociologia Rural. v. 43, n. 1. p. 120-134.
Silva, W. V.; Fontanini, C. A. C.; Del Corso, J. M. (2007); “Garantia da qualidade do café solúvel com o uso do gráfico de controle de somas acumuladas”, Revista Produção On-Line. v. 7, n. 2. p. 43-63.
Soares, I. G.; Castelar, I. (2003); Econometria aplicada com o uso de EViews. Fortaleza: UFC/CAEN.
Souza, A. M. (1991); Aplicação e Performance da Análise de Intervenção em Séries Macroeconômicas Brasileiras. Monografia de Especialização (UFSM).
Souza, F. M.; Lopes, L. F. D. (2009); “Previsão de demanda de leitos hospitalares por meio de análise de Séries Temporais”, Revista Ciência e Natura. v. 31, n. 1. jun. p. 33-47.
Vicini, L.; Souza, A. M. (2007); “Geração de subsídios para a tomada de decisão na cadeia produtiva da bovinocultura do Brasil”, GEPROS – Gestão de Produção, Operações e Sistemas. Ano 2, v. 4. mai./jun. p. 49-64.
Zanela, A.; Lima, de S.; Lopes, L. F. D. (2007); “Identificação de fatores que influenciam na satisfação dos clientes de um clube recreativo por meio de análise fatorial”, GEPROS – Gestão de Produção, Operações e Sistemas. Ano 2, mai./jun. 2007. p. 167-176