1. Introdução
O crescimento econômico e o acirramento da competição estão desencadeando uma busca na melhoria da qualidade e produtividade dos processos produtivos e, conseqüentemente, aperfeiçoamentos nos produtos finais. Atualmente, a sobrevivência do setor industrial está substancialmente baseada na melhoria contínua de seus processos e produtos.
Neste contexto, diante da velocidade com que as mudanças tecnológicas se apresentam, a utilização de ferramentas estatísticas, cada vez mais específicas, direcionadas ao aperfeiçoamento da qualidade, têm sido incrementada na maior parte das organizações para elevar os níveis de qualidade, buscando reduzir custos, permitindo, em longo prazo, a sobrevivência e o aumento da participação no mercado.
Nesta pesquisa, utilizaram-se dados provenientes de técnicas de controle estatístico do processo com abordagem univariada. Os gráficos de controle mais frequentemente utilizados pelas empresas são gráficos de controle univariados, pois sempre tiveram uma ampla divulgação na literatura e seu emprego sempre foi mais acessível para os operadores. A média móvel ponderada exponencialmente (EWMA - Exponentially Weighted Moving Average) tem encontrado aplicações em um grande número de diferentes áreas. É conhecida por evidenciar prognósticos rápidos e eficientes. Monitora pequenas mudanças na média de uma seqüência de observações independentes de sua normalidade. Outra ferramenta é a Análise de Componentes Principais (ACP), uma técnica estatística de análise multivariada que transforma linearmente um conjunto original de variáveis num conjunto substancialmente menor de variáveis não correlacionadas que contém a maior parte da informação do conjunto original. Deve-se ressaltar que a análise de componentes principais proporciona a redução das variáveis a serem investigadas, mas principalmente verifica a identificação da variável ou conjunto de variáveis possivelmente causadoras de instabilidade no sistema.
Nesta pesquisa, o problema proposto é de analisar a eficiência do controle multivariado através de dados levantados no CEP implantado na empresa em estudo; e, mostrando a contribuição dos gráficos de controle EWMA e Análise dos Componentes Principais para a melhoria contínua da qualidade.
Assim, a presente pesquisa apresenta uma análise de controles multivariados, sem que haja necessidade de ajuste em todas as variáveis envolvidas no sistema, mas somente naquelas que apresentam uma situação de instabilidade, utilizando dados levantados em processos com controles univariados e multivariados.
1.1 Objetivos
Mostrar a importância da análise multivariada no Controle Estatístico do Processo, por meio da Análise de Componentes Principais.
Utilizar o Gráfico de Controle EWMA para que auxilie na avaliação da estabilidade do processo, a fim de obter um maior controle sobre os processos multivariados.
1.2 Delimitação da pesquisa
Este trabalho apresenta duas técnicas multivariadas úteis, ACP e EWMA, para identificar, monitorar e ajustar um processo produtivo, sendo que os dados são provenientes de um processo que utiliza CEP para controle, de forma univariada.
O emprego de controle multivariado envolve facilidades na análise de uma grande quantidade de dados amostrais, principalmente quanto a variáveis fora de controle que necessitam de ajustes imediatamente, permitindo às empresas aumentarem os lucros através da redução dos custos (desperdícios e retrabalhos no processo).
2. Controle estatístico de processo
2.1 Histórico
O rápido crescimento de tecnologias e o uso de computadores para o monitoramento dos processos produtivos em tempo real, com menores custos, possibilita monitorar, simultaneamente, várias características da qualidade ou variáveis de processo correlacionadas.
O Dr. Walter A. Shewhart, do Bell Telephone Laboratories, enquanto estudava os dados de um dos processos de seu laboratório, na década de 20, foi o primeiro a formalizar a distinção entre variação controlada e não controlada, que corresponde ao que chamamos de causas comuns e causas especiais. Ele desenvolveu uma ferramenta simples, mas poderosa, para separar esses dois tipos de causas, que chamou de carta de controle.
Desde essa época, as cartas de controle têm sido usadas com sucesso numa grande variedade de situações de controle de processo. A experiência tem mostrado que as cartas de controle efetivamente evidenciam causas especiais de variação quando elas aparecem, e refletem a extensão da variação de causas comuns que devem ser reduzidas com a melhoria do processo.
Os métodos estatísticos são ferramentas eficazes para a melhoria da qualidade do processo produtivo e redução de seus defeitos. Para Kume (1993), os métodos estatísticos são abordagem direta e, são muito eficientes, oferecendo objetividade e exatidão, dando maior importância aos fatos do que aos conceitos abstratos.
2.2 Fundamentos do Controle Estatístico de Processos
O principal elemento do CEP é a carta de controle de processo, que através de um histórico de dados, permite identificar o comportamento do processo ao longo do tempo e detectar a incidência de causas especiais, permitindo ações que previnam e evitem sua reincidência. O CEP possibilita um controle eficaz da qualidade, feito pelo próprio operador e em tempo real. Assim, promove-se um aumento do comprometimento do colaborador com a qualidade do item que está sendo produzido pelo processo por ele controlado. As atividades de supervisão são reduzidas, permitindo à gerência centralizar seus esforços em ações que visem à melhoria dos processos de um modo geral (PIRES, 2000).
O CEP fornece uma descrição detalhada do comportamento do processo, identificando sua variabilidade e possibilitando seu controle ao longo do tempo, através da coleta continuada de dados e da análise e correção de possíveis causas especiais, responsáveis pela instabilidade do processo em estudo. No CEP, o monitoramento do processo pode ser executado pelos próprios operadores, possibilitando uma rápida identificação de anomalias, além de proporcionar maior consistência e previsibilidade no processo, com vistas à atuação e tomada de decisões na busca de melhorias (DIAS, 2004).
As Cartas de Controle utilizam, como dados de entrada, medições realizadas de uma determinada característica de qualidade ou parâmetro de processo que influencie na qualidade dos produtos manufaturados. As medições são realizadas em pontos espaçados de tempo ou volume de produção, sendo registradas graficamente nas cartas, depois comparadas contra limites de controle pré-estabelecidos (MICHEL, 2001).
Segundo Montgomery (2004), há pelo menos cinco boas razões para sua popularidade:
- o gráfico de controle é uma técnica comprovada para a melhoria da produtividade, reduzindo sucatas e retrabalho e, consequentemente, aumento de produtividade e baixo custo do produto;
- são eficazes na prevenção de defeitos, pois, com o processo sob controle, a organização produz certo da primeira vez;
- com os gráficos de controle, o operador intervém sobre o processo com a certeza, de um fundamento teórico e provável, de que o processo está fora de controle, ou seja, “se não está quebrado, não conserte”;
- fornecem informações de diagnóstico. Para um operador ou engenheiro experiente, pode-se tirar, por meio dos pontos do gráfico de controle, uma possível mudança no processo que melhore seu desempenho;
- fornecem informações sobre a capacidade do processo, informam os valores de seus parâmetros mais importantes e também a estabilidade ao longo do tempo, permitindo que se estime a capacidade do processo em atender às especificações dos clientes.
Segundo Grant e Leavenworth (1986) e depois Pires (2000), as causas comuns atuam continuamente sobre o processo, sendo de natureza essencialmente aleatória e de difícil controle. Atuar sobre causas comuns normalmente requer investimentos na melhoria de equipamentos, troca de matérias primas ou treinamento de colaboradores. Uma vez mantidas em níveis razoáveis, as causas comuns não afetam de maneira nociva a qualidade dos itens manufaturados.
2.3 Gráficos de Controle Multivariado
A diferença entre o controle univariado e o multivariado é o aumento da complexidade e dos níveis de automação dos processos produtivos, auxiliado pela crescente disponibilidade de suporte computacional. Esse fato é responsável pela expansão do controle multivariado dentro das indústrias monitorando simultaneamente as várias características de qualidade, também chamadas de variáveis do processo apresentada por (MONTGOMERY, 2004).
Os gráficos utilizados para avaliar a estabilidade do processo são o de Shewhart e o de Médias Móveis Exponencialmente Ponderadas – MMEP - em inglês (EWMA) “Exponentially Weighted Moving Average”. O Shewhart tem como objetivo detectar grandes variações na média do processo, enquanto que o EWMA é mais utilizado para capturar pequenos desvios da média.
O gráfico de controle EWMA foi apresentado inicialmente por Roberts (1959) e introduzido por Wortham e Henrick (1972) para aplicações em processos em indústria química, finanças e outras situações onde amostras unitárias por período de tempo estivessem disponíveis. Esse gráfico é uma alternativa para aos gráficos de Shewhart quando se pretende identificar pequenos deslocamentos na média do processo.
A observação unitária pode ser uma média, um valor individual, uma fração ou uma observação similar (Wadsworth, 2001). Assim, a estatística EWMA pode ser utilizada tanto para dados individuais quanto para subgrupos racionais.
Robinson e Ho (1978), Crowder (1987, 1989) e Lucas e Saccucci (1990) apresentaram procedimentos numéricos e avanços que permitiram que os gráficos EWMA se tornassem mais simples de serem utilizados e operados. O desempenho dos gráficos EMWA é praticamente equivalente ao Gráfico de Somas Acumulativas (CUSUM), com a diferença de que o EWMA é mais fácil para construir e operar.
Woodall e Maragah (1990) complementam que para a aplicação prática os gráficos EWMA são mais fáceis de serem compreendidos pelos usuários devido a sua semelhança com os gráficos de Shewhart. Segundo Hunter (1986), as principais diferenças entre os gráficos de Shewhart, CUSUM e EWMA dizem respeito a maneira com que cada um dos métodos utiliza as informações coletadas no processo. Enquanto o gráfico Shewhart depende unicamente do último ponto coletado, o CUSUM atribui um peso semelhante para todos os pontos plotados no gráfico e no EWMA o peso das amostras mais recentes é o maior e o das amostras anteriores é sucessivamente menor, decrescendo de forma geométrica da mais recente até a antiga.
O gráfico de controle EWMA é uma média ponderada de todas as médias amostrais anteriores, pode ser escrita como:
![]()
O gráfico se comporta como um gráfico EWMA quando os dados coletados estão na região próxima à estatística inicial e como um gráfico Shewhart em outras regiões (ZAGO,2009).
Após o gráfico de controle EWMA ter percorrido diversos períodos de tempo, os limites de controle aproximar-se-ão dos valores de posição fixa, dados:

Para Montgomery (2004), consideram-se os limites de controle simétricos em relação a zero, ou seja, LSC = LIC, com o L = 3 estes limites são equivalentes aos limites de controle 3σ do gráfico de Shewhart. Recomenda-se usar diretamente os limites de controle LSC e LIC para valores pequenos de i. Isto melhora muito o desempenho de um gráfico de controle em detectar imediatamente um processo fora do objetivo após a EWMA ser iniciada.
O processo será considerado sob controle se todos os pontos estiverem dentro dos limites estabelecidos pelas Equações do LIC e do LSC. Geralmente um controle combinado dos gráficos de Shewhart e EWMA é utilizado, sendo que o primeiro avalia o sistema por meio do ![]() , procurando por grandes variações e, o segundo é usado para avaliar pequenas discrepâncias (SOUZA, 2000).
, procurando por grandes variações e, o segundo é usado para avaliar pequenas discrepâncias (SOUZA, 2000).
2.4 Análise de Componentes Principais (ACP)
A Análise de Componentes Principais é uma técnica de análise exploratória multivariada que transforma um conjunto de variáveis correlacionadas num conjunto menor de variáveis independentes, combinações lineares das variáveis originais, designadas por Componentes Principais. Descrita desta forma, a ACP geralmente é encarada como um método de redução de dados, mas além desse objetivo, a ACP permite resumir a informação de várias variáveis correlacionadas em uma ou mais combinações lineares independentes (Componentes Principais) que resumem a maior parte das informações contidas nas variáveis originais. Essas CPs podem depois serem utilizadas como índice ou indicadores que resumem as informações contidas nas variáveis. O autor cita um exemplo da utilização dessa técnica nas bolsas de valores, onde os analistas costumam analisar as 20 maiores empresas com volume de negócios, todas 20 estão contidas em um único índice (essas 20 empresas formam a Componente Principal), pois é mais fácil para os analistas avaliar o comportamento de uma única variável do que de 20 variáveis independentes destas empresas e mais ainda as outras quase 500 ações menos trabalhadas (MOROCO, 2003).
A ACP foi originalmente concebida por Pearson (1901) e, posteriormente, desenvolvida e aprimorada por Hotelling em 1933. Basicamente, a ACP consiste em uma técnica estatística que permite reduzir um modelo multivariado a um conjunto de poucas componentes, não correlacionadas, que carregam a maior parte da informação contida no modelo original.
Para a determinação das componentes principais, é necessário calcular a matriz de variância-covariância (![]() ) ou a matriz de correlação (R), encontrar os autovalores e os autovetores e, por fim, escrever as combinações lineares que serão as novas variáveis, denominadas de componentes principais (SOUZA, 2000). Para o estudo deste item, segue-se o esquema na Figura 1.
) ou a matriz de correlação (R), encontrar os autovalores e os autovetores e, por fim, escrever as combinações lineares que serão as novas variáveis, denominadas de componentes principais (SOUZA, 2000). Para o estudo deste item, segue-se o esquema na Figura 1.
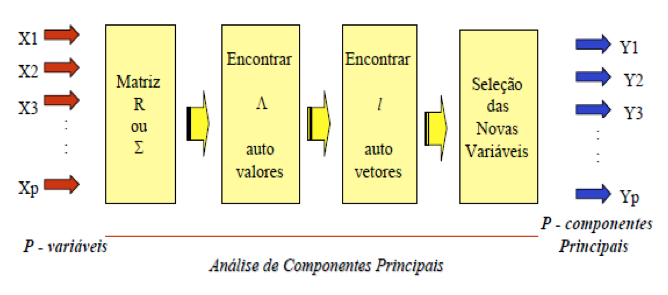
Fonte: (Souza, 2000)
Figura 1 - Esquema da aplicação da Análise de Componentes Principais
A Análise de Componentes Principais (CPs) é uma técnica estatística utilizada para resumir informações em conjuntos de dados multivariados. Considere um conjunto de dados composto de realizações de p variáveis aleatórias. Tal conjunto de dados possui p CPs, sendo cada CP formado por uma combinação linear distinta das p variáveis aleatórias originais. Essas combinações são determinadas através de manipulações algébricas na matriz de covariâncias das p variáveis, conforme apresentado mais adiante. Cada CP captura uma direção de variabilidade do conjunto de dados originais. As direções capturadas por cada CP são ortogonais entre si. Isso equivale a dizer que os CPs são variáveis aleatórias independentes (ROSA, 2001).
A análise de componentes principais tem como objetivo explicar a estrutura de variâncias e covariâncias de um conjunto de variáveis de interesse através de combinações lineares das variáveis X1, X2 ,LXpque são correlacionadas entre si (MINGOTI, 2005). Ainda Johnson e Wichern (2002) e Mingoti (2005) comentam que geometricamente, essas combinações lineares representam a seleção de um novo sistema de coordenadas obtidas através da rotação do sistema origin al, tendo como coordenadas os novos eixos Y1 ,Y2, L,Yp.
Geometricamente, os CPs podem ser representados por um sistema de eixos ortogonais com origem posicionada na média do conjunto de dados. O primeiro CP segue a direção de maior variabilidade dos dados. O segundo CP segue a segunda direção de maior variabilidade, ortogonal ao primeiro CP. Os demais CPs são posicionados no espaço p-dimensional seguindo a mesma lógica. À primeira e assim por diante (LOPES, 2001).
Suponha duas variáveis aleatórias X1, X2, seguindo uma distribuição Normal bivariada N2(![]() ,
, ![]() ), com vetor de médias dado por
), com vetor de médias dado por![]() e matriz de covariâncias
e matriz de covariâncias ![]() . A função de densidade de N2(
. A função de densidade de N2(![]() ,
, ![]() ) é dada pela equação da elipse centrada em
) é dada pela equação da elipse centrada em ![]() :
:
![]() ,
,
onde x denota o vetor que contém as variáveis aleatórias X1 e X2. Os eixos da elipse em (3) são dados por ![]() , i=1,2 (ROSA, 2001).
, i=1,2 (ROSA, 2001).
Os CPs ![]() estão posicionados nas direções dos eixos da elipse de densidade constante, conforme ilustrado na Figura 2.
estão posicionados nas direções dos eixos da elipse de densidade constante, conforme ilustrado na Figura 2.
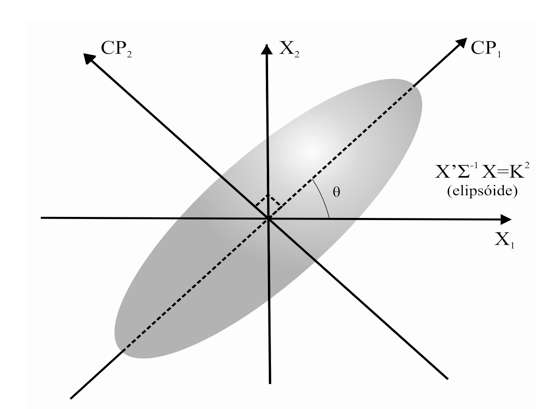
Fonte: Adaptado de Lopes (2001)
Figura 2 – Representação gráfica dos autovalores e autovetores.
Segundo Johnson e Wichern (1992) e depois Lopes (2001), o primeiro componente corresponde ao maior eixo da elipsóide (CP1) e o comprimento desse eixo é proporcional a ![]() . O eixo de menor variância (CP2) é perpendicular ao eixo maior. Esse eixo chama-se segundo componente principal e seu comprimento é proporcional a
. O eixo de menor variância (CP2) é perpendicular ao eixo maior. Esse eixo chama-se segundo componente principal e seu comprimento é proporcional a ![]() . Assim, a análise dos componentes principais toma os eixos X1 e X2 e coloca-os na direção da maior variabilidade.
. Assim, a análise dos componentes principais toma os eixos X1 e X2 e coloca-os na direção da maior variabilidade.
3. Procedimentos metodológicos
A finalidade deste trabalho será a monitoração por meio de ferramentas estatísticas (gráficos de controle) univariado e multivariado de uma linha de produção, no caso, uma única marca de cigarro da empresa “X”, produzida no mês de setembro de 2010.
No presente estudo, será necessário o emprego de técnicas de monitoramento de produção univariada para suporte aos gráficos de controle multivariados, onde serão utilizados os programas Statistica 7.0 e o SPSS 16, programas estes exclusivamente dedicados às rotinas estatísticas.
O primeiro passo será a determinação das medidas descritivas das quatro variáveis envolvidas no processo. Logo em seguida, será elaborado o Histograma das variáveis com a finalidade de verificar se as mesmas apresentam Distribuição Normal (Teste de Kolmogorov-Smirnov). Na sequência, serão utilizados os gráficos univariados para visualizar o comportamento do processo. A próxima etapa será a construção da matriz de correlação (Correlação de Pearson) e a aplicação do teste de Kaiser-Meyer-Olkin ou KMO para verificar a adequação das variáveis para a realização da análise de componentes principais.
O KMO é a razão da soma dos quadrados das correlações de todas as variáveis dividida por essa mesma soma, acrescentando a soma dos quadrados das correlações parciais de todas as variáveis. Quando as correlações parciais forem muito pequenas, o KMO terá valor próximo de 1 e indicará perfeita adequação dos dados para a Análise de Componentes Principais e análise fatorial (PEREIRA, 2001).
Após essa etapa, utilizaremos o gráfico ![]() nas Componentes Principais, para verificar a existência de amostras fora de controle ou em não conformidade. O passo final é a aplicação do gráfico de controle da Média Móvel Exponencialmente Ponderada - EWMA – (Exponentially Weighted Moving Average) na ou nas componentes principais, pois este é um excelente gráfico quando se necessita diagnosticar pequenas mudanças nos valores das amostras do processo estudado.
nas Componentes Principais, para verificar a existência de amostras fora de controle ou em não conformidade. O passo final é a aplicação do gráfico de controle da Média Móvel Exponencialmente Ponderada - EWMA – (Exponentially Weighted Moving Average) na ou nas componentes principais, pois este é um excelente gráfico quando se necessita diagnosticar pequenas mudanças nos valores das amostras do processo estudado.
3.1 Caracterização da empresa
No presente trabalho, os dados foram levantados no setor de produção de uma empresa do ramo fumageiro localizada no estado do Rio Grande do Sul. A indústria do fumo é o conjunto de empresas que atuam na elaboração do tabaco em seus derivados, sendo o produto não comestível mais plantado e comercializado no mundo, tão importante para a economia brasileira que suas folhas estão no brasão da república. (AFUBRA, 2011).
No Brasil, a cadeia do fumo comporta todos os elos da cadeia produtiva do setor: do plantio ao processamento do fumo em folha e fabricação de cigarros e de outros derivados do tabaco, como charutos e cigarrilhas.
Segundo a AFUBRA (2011), na safra 2009/2010, na região sul do Brasil foram plantados no Brasil 370.830ha de fumo, sendo envolvidas 870.250 pessoas, com uma renda bruta na safra de 4,350 bilhões de reais, gerando, em toda a cadeia produtiva, 2,530 milhões de empregos no Brasil.
A cultura é extremamente taxada em impostos, nas últimas três safras proporcionou aos cofres públicos 7,860 bilhões, 8,496 bilhões e 8,426 bilhões de reais em impostos respectivamente (AFUBRA, 2011).
Os fumos cultivados são do tipo Virgínia ou Burley. A alta produtividade e estabilidade do mercado, em que os preços mínimos são estabelecidos antes da safra, fazem dessa a principal atividade econômica das pequenas propriedades espalhadas por mais de 700 municípios nos três estados da região Sul (AFUBRA, 2011).
3.2 Variáveis do estudo
O processo produtivo em estudo é composto de quatro variáveis monitoradas na fase de fabricação do cigarro. Conforme mencionado anteriormente, cada empresa tem as suas técnicas próprias de transformação do tabaco em cigarro. A fabricação, embora toda automatizada, sofre influência de alguns fatores. A umidade e temperatura são monitoradas a todo instante, pois influenciam no sabor e no desempenho da linha de produção. Nesse estudo, utilizou-se uma única marca de cigarro em uma única linha produtiva. As medições das amostras são realizadas de forma totalmente automatizada, onde retira-se cinco amostras (cigarro pronto) da linha de produção em intervalos que variam de 20 a 40 minutos. Essa amostra de cigarros passa automaticamente para um testador eletrônico ao lado da linha produtiva, onde o laboratório automatizado testa um a um dos cinco cigarros informando o seu resultado a um banco de dados. Após leitura e interpretação dos resultados, o operador toma a decisão de agir corretivamente se necessário ou de até parar a linha produtiva dependendo da gravidade da não conformidade.
As quatro variáveis a serem estudadas são: RTD (Resistence to Draw), peso, ventilação e circunferência, onde cada marca de cigarro tem suas especificações determinadas no projeto de produto.
A variável RTD (Resistence to Draw) refere-se à pressão que se faz para tragar o cigarro, sua unidade de medida é em mm.w.g. (é a pressão que determinada coluna d'água exerce na base), quanto maior a força necessária para sugar a fumaça, mais forte é o sabor do cigarro.
O peso é o valor total do cigarro pronto expresso em miligramas, também influi no sabor, quanto mais tabaco dentro do cigarro, maior será a pressão interna, maior será a força necessária para tragá-lo, mais forte será o sabor.
A circunferência é medida do corpo do cigarro, ela é verificada em milímetros. Uma circunferência maior, mais tempo necessário para fumar um cigarro.
Ventilação é a percentagem de transposição do ar, é medida pela percentagem de ar que consegue transpor a ponteira (tiping). Ela é determinada pelo tipo de filtro e papel usado por cada marca, mais facilidade do ar transpor a ponteira, mais acentuado é o sabor do cigarro.
4. Apresentação e análise dos resultados
O presente estudo refere-se a amostras referentes a todo mês de setembro de 2010 de uma linha produtiva. Essa amostra mensal é composta de 20940 medições, sendo 5235 medições para cada uma das 4 variáveis, fez-se a média das 5 mostras, totalizando 1047 médias para cada uma das 4 variáveis.
Após o tratamento dos dados, a fim de transformá-los em uma planilha Excell reconhecida para uso no Statistica 7.0 e SPSS 16, estuda-se, através da estatística descritiva, o comportamento das variáveis. Estas são mostradas na Tabela 1, onde se tem: o número de amostras de cada variável, a Média, o Desvio-padrão, o Mínimo e Máximo de todos os valores das amostras.
1º Passo: Medidas Descritivas das varáveis em estudo
Tabela 1 - Estatística Descritiva
Variável |
n |
Média |
Desv. Padrão |
Mínimo |
Máximo |
RTD |
5235 |
95,82 |
5,4680 |
61,00 |
131,00 |
Peso |
5235 |
959,45 |
27,6146 |
856,00 |
1052,000 |
Ventilação |
5235 |
43,12 |
3,2345 |
31,50 |
53,800 |
Circunferência |
5235 |
24,45 |
0,08195 |
23,90 |
25,25 |
Num primeiro momento, será realizado o Teste de Normalidade (Teste de Kolmogorov-Smirnov, para amostras acima de 2000 unidades) das variáveis, onde observou-se que todas apresentaram proximidade com a distribuição normal necessárias para a utilização das mesmas no trabalho (p > 0,05).
2º Passo: Histograma e Teste de Normalidade das variáveis
As figuras na próxima página apresentam o histograma das variáveis estudadas:
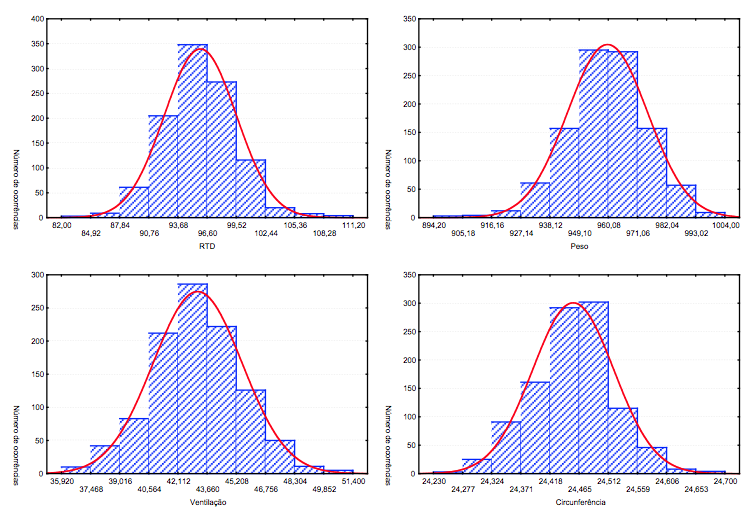
Figura 3 - Histogramas das Variáveis RDT, Peso, Ventilação e Circunferência
Nas figuras acima, observa-se que a RTD, Peso, Ventilação e Circunferência apresentam o comportamento de uma distribuição normal. Portanto, o requisito de normalidade (Normalidade pelo Teste de Kolmogorov-Smirnov, p > 0,05) é satisfeito pelas quatro variáveis, sendo que é possível aplicar o Controle Estatístico de Processo ao grupo de amostras da empresa em estudo.
Em seguida, foi elaborado o Gráfico de Controle de ![]() e R das quatro variáveis, para verificar se os mesmos possuem pontos fora de controle ou em não conformidade.
e R das quatro variáveis, para verificar se os mesmos possuem pontos fora de controle ou em não conformidade.
3º Passo: Gráficos de Controle Univariado

Figura 4 – Gráfico ![]() e R da variável RTD
e R da variável RTD
Na Figura 4, verifica-se que no Gráfico ![]() do RTD apresenta inúmeros pontos fora de controle e que no Gráfico R apresentar alguns valores em não conformidade. Conforme mencionado anteriormente, esses limites são estatísticos de padrão 3σ de controle de qualidade, não sendo os limites de projeto de produto utilizados na empresa.
do RTD apresenta inúmeros pontos fora de controle e que no Gráfico R apresentar alguns valores em não conformidade. Conforme mencionado anteriormente, esses limites são estatísticos de padrão 3σ de controle de qualidade, não sendo os limites de projeto de produto utilizados na empresa.
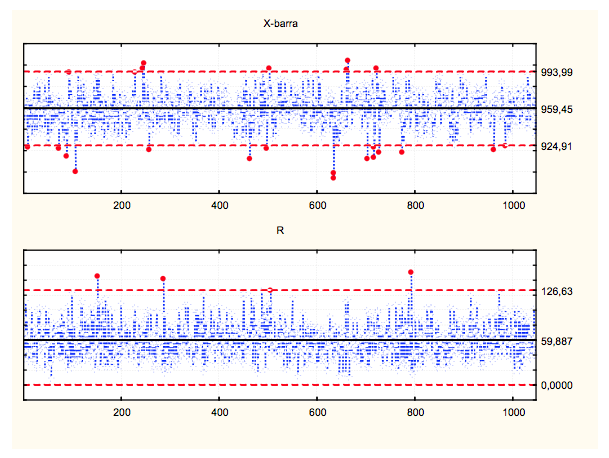
Figura 5 – Gráfico ![]() e R da variável Peso
e R da variável Peso
Observa-se que no Gráfico ![]() do Peso apresenta alguns pontos fora de controle e que no Gráfico R apresentar 4 amostras não-conformes.
do Peso apresenta alguns pontos fora de controle e que no Gráfico R apresentar 4 amostras não-conformes.
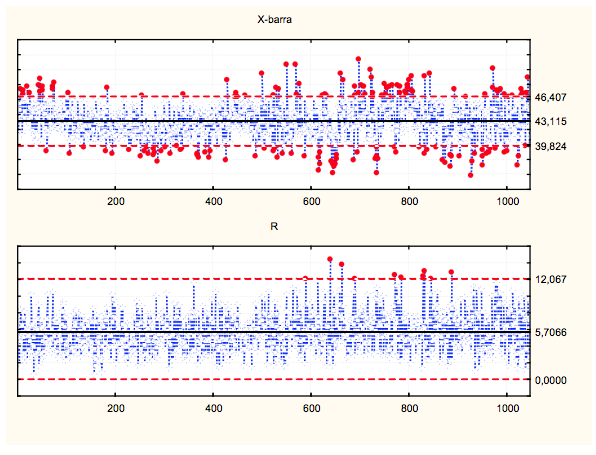
Figura 6 – Gráfico ![]() e R da variável Ventilação
e R da variável Ventilação
Pode-se verificar que no Gráfico ![]() e R da ventilação apresentam inúmeros pontos fora de controle ou não conformes.
e R da ventilação apresentam inúmeros pontos fora de controle ou não conformes.

Figura 7 – Gráfico ![]() e R da Variável Circunferência
e R da Variável Circunferência
Pode-se verificar que no Gráfico ![]() da circunferência apresenta inúmeros pontos fora de controle em todo período de análise do processo e, no Gráfico R, apresenta alguns valores em não conformidade.
da circunferência apresenta inúmeros pontos fora de controle em todo período de análise do processo e, no Gráfico R, apresenta alguns valores em não conformidade.
4º Passo: Matriz de Correlação e Teste KMO
O teste KMO foi significativo, obtendo como resultado KMO=0,488 (p=0,0001) satisfazendo a pressuposição de que as variáveis poderão ser agrupadas pelas componentes principais.
5º Passo: Determinação do número de componentes principais
A fim de identificar as variáveis que apresentam maior variabilidade, ou, as possíveis causadoras da instabilidade no sistema, utilizam-se as primeiras componentes, que são representadas pelos maiores autovetores. Neste caso, a seleção das componentes será feita utilizando os critérios de Kaiser (1960) que diz que, em geral, uma explicação em torno de 70% são suficiente para que as componentes sejam selecionadas e o Critério gráfico de Cattel (1966) vem a ser um critério alternativo.
Segundo os critérios de seleção, segundo Kaiser (1960), escolhem-se apenas os autovalores maiores do que 1, ou que representem em torno de 70% da variância acumulada.
Tabela 2 – Resultados da Soma dos Quadrados Extraídos (Extração da Componente Principal)
Componente |
Autovalor Inicial |
Soma dos Quadrados Extraídos |
|||||
Valor |
% da Variância |
% da Var. Acumulada |
Total |
% da Variância |
% da Var. Acumulada |
||
CP |
1 |
1,524 |
38,097 |
38,097 |
1,524 |
38,097 |
38,097 |
2 |
1,164 |
29,096 |
67,193 |
1,164 |
29,096 |
67,193 |
|
3 |
,775 |
19,387 |
86,580 |
|
|
|
|
4 |
,537 |
13,420 |
100,000 |
|
|
|
|
Observando a Tabela 2, serão escolhidas as duas primeiras componentes com uma explicação total do conjunto de dados de 67,193%, sendo que a primeira CP1 acumula 38,097% das características das variáveis e a CP2 29,096%, num total de 76,193%.
6º Passo: Correlação das variáveis iniciais e as componentes principais
Quadro 1 – Matriz de correlação das variáveis com as componentes principais
Valor de R Significância |
Componentes |
|
CP1 |
CP2 |
|
RTD |
-0,087 |
0,909 |
p = 0,001 |
p = 0,001 |
|
Peso |
0,696 |
0,509 |
p = 0,001 |
p = 0,001 |
|
Ventilação |
0,781 |
-0,162 |
p = 0,001 |
p = 0,001 |
|
Circunferência |
0,650 |
-0,230 |
p = 0,001 |
p = 0,001 |
|
Observamos no Quadro 1 que a CP1 incorporou as características das variáveis: peso, ventilação e circunferência, e a CP2 incorporou as características da variável RTD.
7º Passo: Análise das componentes principais
4.1 Análise gráfica da primeira CP através dos gráficos 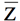 e EWMA
e EWMA
A Figura 8 apresenta a análise do gráfico ![]() da primeira Componente Principal, pode-se observar vários pontos em vermelho, estes pontos estão fora dos limites de 3σ, portanto causam instabilidade ao processo.
da primeira Componente Principal, pode-se observar vários pontos em vermelho, estes pontos estão fora dos limites de 3σ, portanto causam instabilidade ao processo.

Figura 8 - Gráfico X-barra para a primeira componente principal
A fim de melhor analisar os gráficos ![]() , utilizar-se-ão os testes de seqüência (Run Test) aplicados sobre o gráfico EWMA, os quais ajudarão a identificar os pontos fora de controle ou em não conformidade no processo produtivo.
, utilizar-se-ão os testes de seqüência (Run Test) aplicados sobre o gráfico EWMA, os quais ajudarão a identificar os pontos fora de controle ou em não conformidade no processo produtivo.

Figura 9 - Gráfico EWMA para a primeira CP com ![]() = 0,05 e L = 2,5
= 0,05 e L = 2,5
A análise dos gráficos de controle possibilita a identificação se o processo está ou não sob controle, o que significa a ausência de causas especiais de variação. Quando um processo está controlado, ocorre um padrão normal de variação, pois os pontos distribuem-se aleatoriamente em torno da média, indicando a ausência de tendências crescentes ou decrescentes, ciclos, estratificações ou misturas e pontos que ultrapassaram os limites de controle.
Os Testes de Seqüência indicam a existência de algumas variações no processo, as quais devem ser eliminadas ou reduzidas. Para exemplo, temos 9 amostras do mesmo lado do centro: de 216 até 224, de 306 até 314, de 323 até 331, de 721 até 729 e de 1015 até 1023.
Esses resultados, obtidos com os testes anteriores, a primeira componente apresenta vários pontos em não conformidade com os limites de 3σ utilizados no Controle Estatístico do Processo.
4.2 Análise gráfica da segunda CP através dos gráficos ![]() e EWMA
e EWMA
Agora será analisada a segunda CP da mesma forma que a primeira, onde na Figura 10 também constatou-se vários pontos em não conformidade.

Figura 10 - Gráfico ![]() para a segunda componente principal
para a segunda componente principal
Abaixo tem-se o gráfico EWMA com vários pontos vermelhos, também evidenciando a instabilidade do processo na CP2.

Figura 11 - Gráfico EWMA para a segunda CP com ![]() = 0,05 e L = 2,5
= 0,05 e L = 2,5
A segunda componente também mostra a instabilidade que ocorre no processo, ela é tão acentuada como na primeira componente, pois sua variabilidade é tão instável quanto a primeira CP.
Os testes de sequência também indicam a existência de variações no processo. Para exemplo, tem-se 9 amostras do mesmo lado do centro: de 584 até 592, de 778 até 786, de 795 até 803, de 827 até 835, de 958 até 966 e de 1033 até 1041.
Após a análise dos gráficos ![]() e EWMA da primeira e segunda Componente Principal, conclui-se que o processo produtivo apresenta falhas de controle de qualidade, pois em todo período estudado as duas CPs apresentaram ocorrências além dos limites de controle de 3σ.
e EWMA da primeira e segunda Componente Principal, conclui-se que o processo produtivo apresenta falhas de controle de qualidade, pois em todo período estudado as duas CPs apresentaram ocorrências além dos limites de controle de 3σ.
O processo produtivo deve ser revisado, a fim de se verificar as falhas durante a fabricação do produto. Essa etapa deve envolver todos os colaboradores da linha produtiva e a gerência de produção, pois processos e metodologias devem ser revistos e corrigidos.
Por fim, acrescenta-se ainda, que as metodologias das ferramentas ACP e EWMA incrementam e completam o Controle Estatístico de Processo, pois produzem várias informações de variações e instabilidade na linha produtiva, auxiliando tanto o operador como a gerência na tomada de decisões.
5. Consideraçôes finais
O objetivo deste trabalho foi aplicar ferramentas estatísticas multivariadas de Controle Estatístico do Processo para monitorar a eficiência do processo produtivo da empresa “X” na fabricação de cigarros.
Utilizando o auxílio de gráficos de controle univariados e multivariados, verificou-se a caracterização do sistema quanto a sua normalidade e estabilidade.
Neste contexto, a Análise dos Componentes Principais (ACP) é um método estatístico linear que calcula os autovalores e autovetores da matriz de covariância dos dados e, com esse resultado, possibilita a redução dimensional dos dados e a análise dos padrões principais de variabilidade presentes.
Assim, a contribuição da ACP pode ser percebida quando se analisou os valores de variância e o desvio padrão da estimativa. Os valores destas medidas foram calculados pelo modelo usando a primeira componente principal tornando evidentes as falhas do processo produtivo. Além disso, evidenciou o conjunto de variáveis mais significativas causadoras de instabilidade no sistema, satisfazendo o objetivo específico relacionado à importância da análise multivariada no Controle Estatístico do Processo por meio da Análise de Componentes Principais.
O gráfico EWMA aplicado nas Componentes Principais evidenciou as falhas, mesmo pequenas, na linha produtiva, mostrando sua importância para detectar os pequenos desvios da média, auxiliando na avaliação da estabilidade do processo, em termos de obter um maior controle sobre os processos multivariados.
À medida que os desperdícios vão sendo diminuídos, novos padrões de desempenho são alcançados. Assim, a sua eliminação contínua conduz melhoramentos de produtividade e qualidade e redução de custos de produção, contribuindo para uma maior competitividade.
Portanto, pode-se afirmar que os objetivos foram atingidos, pois os resultados da pesquisa evidenciam a não-conformidade das amostras em diversos pontos do processo. Com isso, espera-se ter contribuído para a evolução da abordagem multivariada na análise da qualidade do produto através do monitoramento do processo produtivo.
Referências
AFUBRA. Associação dos Fumiculoteres do Brasil. [Acesso em: 2 de fev. de 2011]. Disponível em: http:// www.afubra.com.br/principal.php?acao=conteudo&u_id=1&i_id=1&menus _site_id=10.
CATTEL, R. B. The scree test for the number of factors. “ Multivariate behavior research”. v.1, p. 245-276, 1966.
CROWDER, S. V. A Simple Method for Studying Run Length Distributions of exponentially Weighted Moving Average Charts. “Technometrics”, p. 393-407, 1987.
______. Design of Exponentially Weighted Moving Average Schemes. Journal of Quality Technology, 21, p. 155-162, 1989.
DIAS, L. C. Sistemática para apoiar a redução de perdas e estabilização de processos. Dissertação (Mestrado Profissionalizante em Engenharia Mecânica). Universidade Federal do Rio Grande do Sul. Porto Alegre, 2004.
GRANT, E.; Leavenworth, R. S. “Statistical Quality Control” . 7th ed. New York: McGraw-Hill, 1986.
GUARNIERI, J. P. Eficiência dos gráficos de controle na detecção de outliers em processos autorregressivos e de médias móveis. (Dissertação em Engenharia de Produção) - Universidade Federal de Santa Maria. Santa Maria, 2010.
HUNTER, J. S. The exponentially weighted moving average. “Journal of Quality Technology”, 18(4), p. 203–210, 1986.
JONHSON, R.A.; WICHERN, D.W. “Applied Multivariate Statistical analysis”. Prentice Hall, 6th ed, 2002.
KAISER, H. F. The application of electronic computers to factor analysis. “Educational and Psychological Measurement”, 20, 141-151,1960.
KLUG, M.; MARSHALL, I.; Viterbo, E. “Gestão da qualidade”. São Paulo, 2003.
KUME, H. “Métodos estatísticos para melhoria da qualidade”. São Paulo:Editora Gente, 1993.
LOPES, L. F. D. Análise de componentes principais aplicada à confiabilidade de sistemas complexos. Tese (Doutorado em Engenharia de Produção). Universidade Federal de Santa Catarina. Florianópolis, 2001.
LUCAS, J.M.; SACCUCCI, M. S. “Exponentially Weighted Moving Average Control Schemes: Properties and Enhancements”. Technometrics, 32, 1-29, 1990.
MONTGOMERY, D. C. “Introdução ao Controle Estatístico da Qualidade”. 4a. ed. Rio de Janeiro: LTC, 2004.
MICHEL, R. Cartas adaptativas de controle: desenvolvimento de metodologia para implementação em processos de manufatura. Dissertação (Mestrado em Engenharia de Produção). Universidade Federal do Rio Grande do Sul. Porto Alegre, 2001.
MICHEL, R. e FOGLIATTO, F. S. Projeto Econômico de Cartas Adaptativas para Monitoramento de Processos. “Revista Produto & Produção”, 2000.
MINGOTI, S.A. “Análise de dados através de métodos de estatística multivariada: uma abordagem aplicada”. Belo Horizonte, Editora da UFMG, 2005.
MOROCO, J. “Análise Estatística com Utilização do SPSS”, Lisboa: Sílabo. 2003.
PEARSON, K. On lines and planes of closed fit to system of point in space. Phil. Mag., v. 6, p. 559 – 572. 1901
PEREIRA, J. C. R. Análise de dados qualitativos: estratégias metodológicas para as ciências da saúde, humanas e sociais. São Paulo: Edusp, 2001.
PIRES, V. T. Implantação do Controle Estatístico de Processos em uma empresa de manufatura de óleo de arroz. (Mestradoo em Engenharia de Produção). Universidade Federal do Rio Grande do Sul. Porto Alegre, 2000.
PITT, H. “SPC for the rest of us: a Personal path to Statistical Process Control”. Massachusets: Addison-Wesley, 1994.
ROBERTS S. W. Control chart tests based on Geometric Moving Averages. “Technometrics”, v.1, 1959.
ROBSON, P.B.; HO, T. Y. Average run lengths of geometric moving average charts by numerical methods. “Technometrics”, v.20, p.85-93, 1978.
ROSA, A. F. P. Método para controle estatístico multivariado de processos em batelada. Dissertação (Mestrado em Engenharia de produção). Universidade Federal do Rio Grande do Sul. Porto Alegre, 2001.
ROSA. A. F. P.; FOGLIATTO, F. S. Cartas de controle multivariadas baseadas em componentes principais. Artigo da ABEPRO. [Aceso em: 5 fev. 2011]. Disponível em: http:// www.abepro.org.br /biblioteca/ENEGEP1999_A0139.PDF.
SOUZA, A. M. Monitoração e ajuste de realimentação em processos produtivos multivariados. Tese (Doutorado Engenharia de Produção) – Universidade Federal Santa Catarina, 2000.
SOUZA, F. M. Estudo do consumo e do número de consumidores de energia elétrica do RS por meio de componentes principais e modelos de previsão. Dissertação (Mestrado em Engenharia de Produção) - Universidade Federal de Santa Maria. Santa Maria, 2011.
WADSWORTH, H. M., et al. “Modern methods for quality control and improvement”. 2nd Edition. New York: John Wiley & Sons, 2001.
WOODALL, W. H., MARAGAH, H. D. Control charts using exponential smoothing techniques. “Technometrics”, v. 32, pp 1-29, 1990.
WORTHAM, A. W.; HEINRICK, G. F. Control charts using exponential smoothing techniques. ASQ “Annual Technical Conference Preceedings”. pp 451-458, 1972.
ZAGO, V. A. Avaliação da aplicação de gráficos de controle com memória em uma indústria de papel e embalagens. (Mestrado em Engenharia de Produção). Universidade Federal de Santa Catarina. Florianópolis, 2009.