Andrés Felipe Avalos, Sergio Aguilar Urrea y Jhon Wilder Zartha
Recibido: 20-07-2010 - Aprobado
Después de realizar la regresión no lineal de cada una de las series a los diferentes modelos se obtuvieron los resultados registrados en las tablas 1, 2, 3, 4 y 5. Los parámetros encontrados por medio del modelo logístico no fueron necesarios para determinar su punto de inflexión ya que este se obtuvo directamente.
Estos datos fueron reemplazados en la segunda derivada de cada modelo para poder determinar el punto de inflexión, los resultados aparecen en las tablas 1, 2, 3, 4 y 5. En estas tablas también se registraron los valores estadísticos R2, DW, F y t obtenidos con cada modelo.
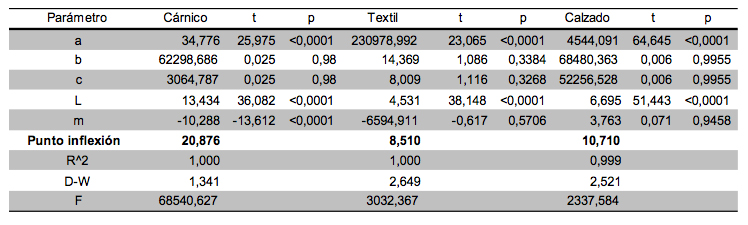
Tabla 1. Resultados obtenidos con el modelo Weibull 5 parámetros

-----
Tabla 2. Resultados obtenidos con el modelo Gaussian 3 parámetros
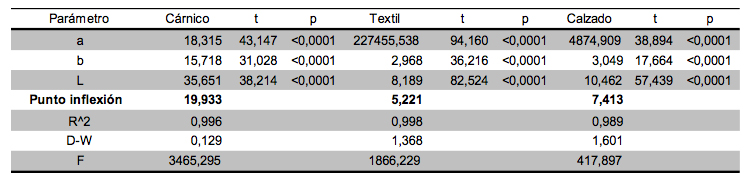
------
Tabla 3. Resultados obtenidos con el modelo Gaussian 5 parámetros.
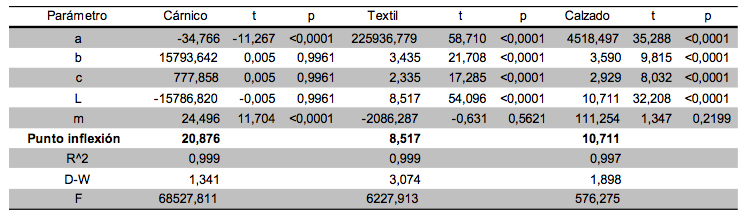
------
Tabla 4. Resultados obtenidos con el modelo Logístico
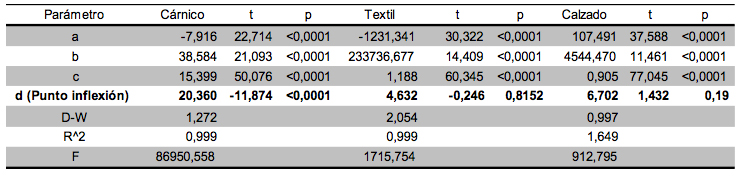
-----
Tabla 5. Resultados obtenidos con el modelo de Bass
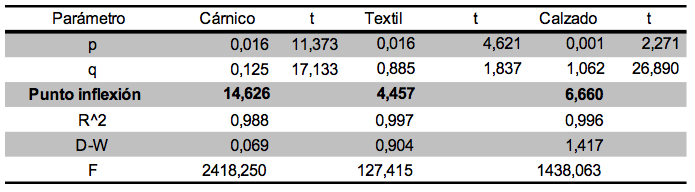
Para el producto cárnico se realizaron los siguientes análisis para determinar cuál era el modelo de mejor ajuste. En primera instancia se analizaron los valores t obtenidos con cada uno de los modelos, se pudo concluir que los modelos Weibull 5 parámetros y Gaussian 5 parámetros no representan adecuadamente el desempeño del producto, ya que en ambos modelos se encontró que |t|< 2. Se analizaron luego los valores de Durbin Watson obtenidos con los modelos Weibull 5 parámetros, Gaussian 5 parámetros y logístico los cuales arrojaron los siguientes resultados 1.341, 1.341 y 1.2722 respectivamente, al buscar en tablas de distribución del valor estadístico Durbin Watson DW se encontró que estos valores no son concluyentes acerca de la autocorrelación residual, en el caso de los modelos Gaussian 3 parámetros y Bass se encontró que existe autocorrelación residual positiva. Adicionalmente el valor del estadístico F más alto se encontró con el modelo logístico, por lo cual se determinó que este era el modelo de mejor ajuste para el producto cárnico.
El modelo de mejor ajuste muestra un valor de punto de inflexión de 20.36, aproximadamente 20 meses, este valor es útil para la organización en los siguientes aspectos:
En el mes 20, de acuerdo con la curva en S de madurez de la tecnología, el estado de la misma es de base y no tecnología emergente ni en crecimiento, por lo que esta información es útil para establecer bases y criterios para la negociación de la misma, es decir, la posición de compra de tecnología después del mes 20 indica que la tecnología puede tener un costo diferente que si estuviera en la fase de emergencia o crecimiento, es decir, al inicio de la curva S. (Ortiz y Pedroza, 2006). Ver Figura 1.
En el mes 20 era importante que ésta empresa hubiera pensado en una innovación incremental o radical derivada de la primera, a su vez, y si considera conveniente reducir los ciclos de innovación, futuras innovaciones en la misma línea de producto se podrían hacer antes del mes 20.
Con relación a la Figura 3 (Pérez, 1992) después del mes 20 no se debe hacer énfasis en mecanismos de privatización del conocimiento ya que en poco tiempo este estará libremente disponible para otros, después de el punto de inflexión se cumple el surgimiento del nuevo paradigma, donde existe alta probabilidad de generación de innovaciones incrementales o radicales por parte de los competidores basadas en los conocimientos disponibles. (Pérez, 1992).
De acuerdo con la Figura 2 (Schilling, 2010), los usuarios de esta innovación están buscando simplicidad, confiabilidad y relación costo-efectividad, por lo que la estrategia a seguir es la de reducción costos para este producto y no estrategias basadas con énfasis en alto contenido de información técnica.
Para el producto Textil se realizaron los siguientes análisis para determinar cuál era el modelo de mejor ajuste. En primera instancia se analizaron los valores t obtenidos con cada uno de los modelos, se puede concluir que los modelos Weibull 5 parámetros, Gaussian 5 parámetros, modelo de Bass y logístico no representan adecuadamente el desempeño del producto, ya que en dichos modelos se encontraron valores de |t|< 2. Se analizaron luego los valores de Durbin Watson obtenidos con los modelos Weibull 5, Gaussian 3 parámetros y logístico los cuales arrojaron los siguientes resultados 2,649, 1,368 y 2,054 respectivamente, al buscar en tablas de distribución del valor estadístico Durbin Watson (DW) se encontró que no existe autocorrelación residual, en el caso de los modelos Gaussian 5 parámetros y Bass se encontró que la prueba no es concluyente en cuanto a la autocorrelación residual. El valor del estadístico F más alto se encontró con el modelo Gaussian 3 parámetros, por lo cual se determinó que este era el modelo de mejor ajuste para el producto textil.
El punto de inflexión del modelo de mejor ajuste es en el mes 5,22 este valor es útil para la organización y las estrategias a seguir serán las mismas que el producto cárnico, teniendo en cuenta que el punto de inflexión para el producto textil es aproximadamente en el mes 5.
Para el producto del sector productivo del calzado se realizaron los siguientes análisis para determinar cuál era el modelo de mejor ajuste. En primera instancia se analizaron los valores t y se pudo concluir que los modelos Weibull 5 parámetros, Gaussian 5 parámetros y logístico no representan adecuadamente el desempeño del producto, ya que se encontraron valores de |t|< 2, Se analizaron luego los valores de Durbin Watson encontrando que ninguno de los modelos presenta autocorrelación residual, mas sin embargo este no es un criterio de descarte definitivo. Según el estadístico t los modelos de mejor ajuste son el Gaussian 3 parámetros y el modelo de Bass, el valor estadístico F de los modelos Gaussian 3 parámetros y el modelo de Bass son 417.89 y 1438.06 respectivamente, por lo que se concluye que el modelo de mejor ajuste para el producto del sector calzado es el modelo de Bass.
El punto de inflexión del modelo de mejor ajuste es 6.6, meses, este valor es útil para la organización y las estrategias a seguir serán las mismas que el producto cárnico, teniendo en cuenta que el punto de inflexión es aproximadamente en el mes 6,6
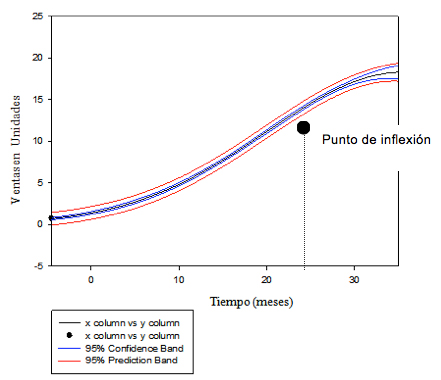
En las figuras 10, 11 y 12 se muestran las curvas del producto cárnico, textil y de calzado respectivamente, en estas gráficas se puede ver la ubicación del punto de inflexión del CVP obtenido con el mejor modelo para cada producto.
Figura 10. Ventas en unidades Vs. Tiempo del producto Cárnico
-----
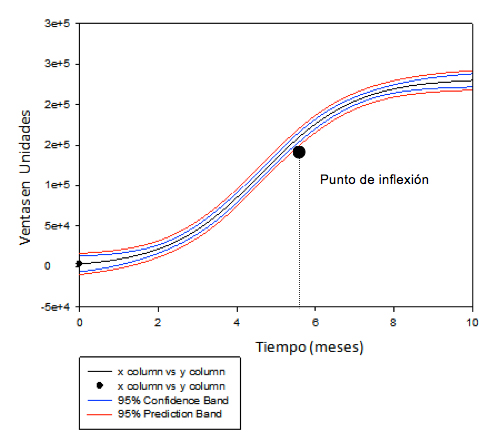
Figura 11. Ventas en unidades Vs. Tiempo del producto Textil
-----
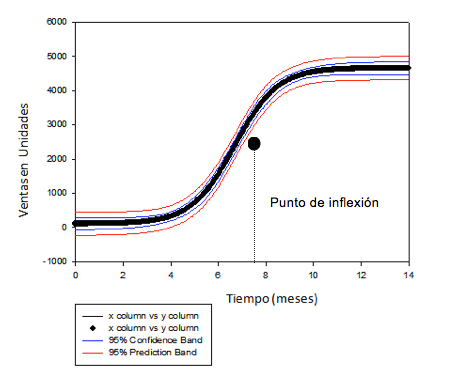
Figura 12. Ventas en unidades Vs. Tiempo del producto Calzado
-----
El estudio de diferentes modelos que describan curvas en S es fundamental para optimizar el proceso de ajuste de los datos a una serie de tiempo.
Es importante desarrollar el mismo proceso a nuevas series de datos, con el fin de aproximarse a un modelo adecuado para cada sector. Además también es necesario seguir realizando la comparación con modelos diferentes.
La metodología utilizada en este artículo es útil para encontrar el punto de inflexión del CVP, pero hace necesaria la utilización de software especializados en procesos matemáticos.
Para complementar este trabajo se debe estudiar el significado de las constantes o parámetros definidos por cada modelo, ya que estas pueden dar información relevante sobre los momentos adecuados para la aplicación de las estrategias de innovación y mercadeo, para el manejo de información y el manejo de recursos.
Se puede buscar otro método para encontrar el punto de inflexión, este proceso puede realizarse por un método numérico o gráfico.
Afuah, A. (1999); La dinámica de la innovación organizacional: El nuevo concepto para lograr ventajas competitivas y rentabilidad. México DF: Oxford University Press México.
Fernández, E. (2005); Estrategias de Innovación. Madrid: Thomson.
Godet, M. (1993); De la anticipación a la acción: manual de prospectiva y estrategia. México DF : Ediciones Alfaomefa.
Kotler, P. (1996); Dirección De Mercadotecnia, Análisis, Planeación, Implementación y Control. México DF: Prentice Hall.
Kucharavy, D. (2007); Application of S-shaped curve. In proc. Triz Future-conference, (kassel university press GmbH), pp. 81-88. Frankfurt: Germany
Kucharavy, D.; De Guio, R. (2009); Logistic Substitution Model and Technological Forecasting. The Triz Journal Part of the Real Innovation Network, ABI/Inform database [02 february 2009]
Leithold, L. (1998); El cálculo. México DF: Oxford University Press.
López, J.; Arroyo, J. (2005); Modelos matemáticos de difusión tecnológica. In proc IX Congreso de Ingeniería de Organización. (Universidad Complutense de Madrid). p. 11. Gijón Spain
Lucio, J.; Usgame D.; Usgame G.; Arenas G.; Bernal E.; Daza S.; Guerrero J.; Pardo M. (2009); Indicadores de ciencia y tecnología, Colombia 2009. Bogotá.
Moraleda, A. (2004); La innovación, clave para la competitividad empresarial. Universia Business Review. N 1 primer trimestre 2004, 128-136 p.
Ortiz, S.; Pedroza, A. (2006); ¿QUÉ ES LA GESTIÓN DE LA INNOVACIÓN Y LA TECNOLOGÍA (GInnT)?. Journal of Technology Management & Innovation. Vol. 1, No. 2.
Pérez, C. (1992); Cambio técnico, restructuración competitiva y reforma institucional en los países en desarrollo. En: El Trimestre Económico, n 223, enero-marzo 1992. 23-64 p.
Pérez, C. (2001); El cambio tecnológico y las oportunidades de desarrollo como blanco móvil. Revista de la CEPAL, No. 75, 115-136
Schilling, M. (2010); Dirección estratégica de la innovación tecnológica. New York. Mc Graw Hill.
Sood, A.; Tellis,G. (2005)Technological Evolution and Radical Innovation. En: Journal of Marketing (ciudad) Vol. 69 (Jul 2005). p.152–168.
White, M; Bruton, G. (2007); The Management of Technology and Innovation: A Strategic Approach. Mason OH: Thomson Higher Education.
Zartha, J.; Castrillón, F.; Avalos, A.; Aguilar, S. (2009); Technological S curves analysis of the diffusion of technological innovations. IAMOT 2009
Zartha, J; Quintero, S. (2008); Modelo Tecnológico por Proyectos: caso de aplicación. Medellín. Universidad Pontificia Bolivariana.
Vol. 32 (2) 2011
[Índice]